题目内容

直线椭圆相交于A，B两点，该椭圆上点P，使得⊿PAB面积等于3，这样的点P共有

(A) 1个             (B) 2个            (C) 3个                (D) 4个

B


解析:

设P1(4cosa,3sina) (0<a<)，即点P1在第一象限的椭圆上，如图，考虑四边形P1AOB的面积S。

　　S===6(sina+cosa)=

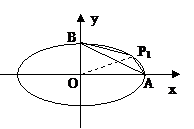    ∴Smax=6

    ∵S⊿OAB=6

    ∴

    ∵<3

    ∴点P不可能在直线AB的上方，显然在直线AB的下方有两个点P，故选B

练习册系列答案
相关题目
已知椭圆的中心在原点，左焦点F1（-2，0），过左焦点且垂直于长轴的弦长为
2
6
3
．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）过（-3，0）点的直线l与椭圆相交于A，B两点，若以线段A，B为直径的圆过椭圆的左焦点，求直线l的方程．
（2013•威海二模）已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为e=
6
3
，过右焦点做垂直于x轴的直线与椭圆相交于两点，且两交点与椭圆的左焦点及右顶点构成的四边形面积为
2
6
3
+2．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设点M（2，0），直线l：y=1，过M任作一条不与y轴重合的直线l1与椭圆相交于A、B两点，过AB的中点N作直线l2与y轴交于点P，D为N在直线l上的射影，若|ND|、
1
2
|AB|、|MP|成等比数列，求直线l2的斜率的取值范围．
如图，已知椭圆
x2
4
+
y2
3
=1上两定点P(-2，0)，Q(1，
3
2
)，直线l：y=-
1
2
x+m与椭圆相交于A，B两点（异于P，Q两点）
（1）求证：kPA+kQB为定值；
（2）当m∈（-1，2）时，求A、P、B、Q四点围成的四边形面积的最大值．

直线椭圆相交于A，B两点，该圆上点P，使得PAB面积等于，这样的点P共有（    ）

(A) 1个             (B) 2个            (C) 3个                (D) 4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网