题目内容
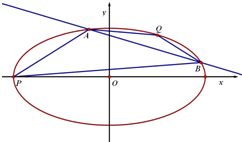 如图,已知椭圆
如图,已知椭圆| x2 |
| 4 |
| y2 |
| 3 |
| 3 |
| 2 |
| 1 |
| 2 |
(1)求证:kPA+kQB为定值;
(2)当m∈(-1,2)时,求A、P、B、Q四点围成的四边形面积的最大值.
分析:(1)因为直线l与椭圆交于A,B两点,所以设出A,B点的坐标,用A,B,P,Q的坐标表示kPA与kQB,因为A,B坐标为直线与椭圆方程联立组成的方程组的解,求出x1+x2,x1x2,代入,kPA+kQB,化简,即为定值.
(2)直线AB把四边形APBQ分成两个三角形,两个三角形都可看做以线段AB为底边,分别以P,Q到AB的距离为高的三角形,用弦长公式求出|AB|长,点到直线的距离公式求出P,Q到AB的距离,再代入三角形面积公式即可.
(2)直线AB把四边形APBQ分成两个三角形,两个三角形都可看做以线段AB为底边,分别以P,Q到AB的距离为高的三角形,用弦长公式求出|AB|长,点到直线的距离公式求出P,Q到AB的距离,再代入三角形面积公式即可.
解答:解:(1)设A(x1,y&1),B(x2,y2),
联立直线与椭圆的方程
⇒4x2-4mx+4m2-12=0⇒
∴kPA+kQB=
+
=
用y1=-
x1+m,y2=-
x2+m代入可得kPA+kQB=
=
=0
(2)SAPBQ=
|AB|×|hP+hQ|=
|
+
|
∵P,Q在直线l两侧
∴SAPBQ=
•
当m=0时∴SAPBQ=3
为其面积的最大值.
联立直线与椭圆的方程
|
|
| y1-0 |
| x1+2 |
y2-
| ||
| x2-1 |
y1(x2-1)+(y2-
| ||
| (x1+2)(x2-1) |
用y1=-
| 1 |
| 2 |
| 1 |
| 2 |
-
| ||||||||
| (x1+2)(x2-1) |
=
| -x1x2+(m-1)(x2+x1)+m-3 |
| (x1+2)(x2-1) |
(2)SAPBQ=
| 1 |
| 2 |
| ||
| 4 |
| 12-3m2 |
| |-2-2m| | ||
|
| |4-2m| | ||
|
∵P,Q在直线l两侧
∴SAPBQ=
| ||
| 4 |
| 12-3m2 |
| 6 | ||
|
当m=0时∴SAPBQ=3
| 3 |
点评:本题主要考查了直线与椭圆相交,弦长公式,点到直线的距离公式,韦达定理等的综合应用.

练习册系列答案
相关题目
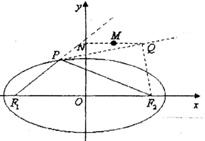 如图,已知椭圆
如图,已知椭圆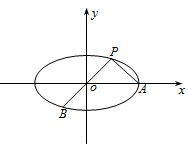 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆
如图,已知椭圆 (2010•武昌区模拟)如图,已知椭圆
(2010•武昌区模拟)如图,已知椭圆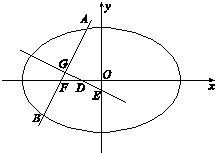 (2013•甘肃三模)如图,已知椭圆
(2013•甘肃三模)如图,已知椭圆