Question

【题目】如图，在圆心角为直角的扇形OAB中，分别以OA，OB为直径作两个半圆，在扇形OAB内随机取一点，则此点取自阴影部分的概率是 ．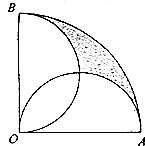

Answer 1

【答案】﹣
【解析】解：如图，设两个半圆的交点为C，且以AO为直径的半圆以D为圆心，连结OC、CD
设OA=OB=2，则弓形OMC的面积为
S弓形OMC=S扇形OCD﹣SRt△DCO= π12﹣ ×1×1= ﹣
可得空白部分面积为S空白=2S半圆AO﹣2S弓形OMC=2× π12﹣（ ﹣1）= +1，
因此，两块阴影部分面积之和为S阴影=S扇形OAB﹣S空白= π22﹣（ +1）= ﹣1
可得在扇形OAB内随机取一点，此点取自阴影部分的概率为P= = = ﹣ ，
所以答案是： ﹣

【考点精析】利用几何概型对题目进行判断即可得到答案，需要熟知几何概型的特点：1）试验中所有可能出现的结果（基本事件）有无限多个；2）每个基本事件出现的可能性相等．