题目内容
有一块铁皮零件,它的形状是由边长为40cm的正方形CDEF截去一个三角形ABF所得的五边形ABCDE,其中AF长等于12cm,BF长等于10cm,如图所示.现在需要截取矩形铁皮,使得矩形相邻两边在CD,DE上.请问如何截取,可以使得到的矩形面积最大?(图中单位:cm)


延长MP交FB于G点,设PG=x,则PM=40-x,
∵PG∥AF,
∴△BPG∽△BAF,
∴
=
,解得BG=
x,
∴NP=CG=30+
x,
∴S矩形PNDM=PM•PN=(30+
x)(40-x)
=-
x2+
x+1200=-
(x-2)2+1200+
(0≤x≤12),
∴当x=2时,函数有最大值为1203
,
此时DN=38cm,DM=
cm.
∵PG∥AF,
∴△BPG∽△BAF,
∴
| BG |
| 10 |
| x |
| 12 |
| 5 |
| 6 |
∴NP=CG=30+
| 5 |
| 6 |
∴S矩形PNDM=PM•PN=(30+
| 5 |
| 6 |
=-
| 5 |
| 6 |
| 10 |
| 3 |
| 5 |
| 6 |
| 10 |
| 3 |
∴当x=2时,函数有最大值为1203
| 1 |
| 3 |
此时DN=38cm,DM=
| 95 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
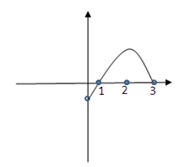
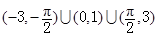
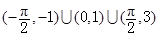
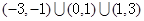
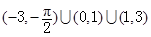
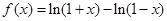 ,
,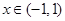 .现有下列命题:
.现有下列命题: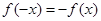 ;②
;②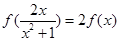 ;③
;③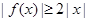 .其中的所有正确命题的序号是( )
.其中的所有正确命题的序号是( )