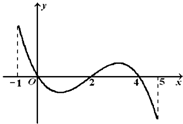
题目内容

当x∈(1,2］时,函数f(x)=恒大于正数a,试求函数y=lg(a2-a+3)的最小值.

答案：
解析：

 思路分析:欲求y=lg(a2-a+3)的最小值,则应知(a2-a+3)的最小值,于是必须确定a的取值范围,进而必须先求出函数f(x)=的最小值.

解:∵y′=()′=,当x∈(1,2］时,y′＜0.

∴f(x)在(1,2］上单调递减,于是f(x)min=f(2)=.

由题意知a的取值范围是a＜,

∴y=lg(a2-a+3)=lg［(a)2+］.

故当a=时,ymin=lg.


练习册系列答案
相关题目
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示． 下列关于f（x）的命题：
x -1 0 4 5
f（x） 1 2 2 1
①函数f（x）的极大值点为0，4；
②函数f（x）在[0，2]上是减函数；
③如果当x∈[-1，t]时，f（x）的最大值是2，那么t的最大值为4；
④当1＜a＜2时，函数y=f（x）-a有4个零点；
⑤函数y=f（x）-a的零点个数可能为0、1、2、3、4个．
其中正确命题的个数是（　　）
已知函数f（x）=x2-4x+3
（1）当x∈[-1，3]时，求函数f（x）的值域；
（2）若关于x的方程|f（x）|-a=0有三个不相等的实数根，求实数a的值；
（3）已知t＞0，求函数f（x）在区间[t，t+1]上的最小值．
已知函数f（x）=
1
3
x3-bx2+2x+a，x=2是f（x）的一个极值点．
（Ⅰ）求f（x）的单调递增区间；
（Ⅱ） 若直线y=2x和此函数的图象相切，求a的值；
（Ⅲ）若当x∈[1，3]时，f（x）-a2＞
2
3
恒成立，求a的取值范围．
当x∈(1,2］时,函数f(x)=恒大于正数a,试求函数y=lg(a2-a+3)的最小值.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网