Question

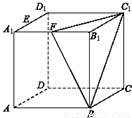如图，在棱长为1的正方体AC₁中，E、F分别为A₁D₁和A₁B₁的中点．
（1）求异面直线AF和BE所成的角的余弦值：
（2）求平面ACC₁与平面BFC₁所成的锐二面角：
（3）若点P在正方形ABCD内部或其边界上，且EP∥平面BFC₁，求EP的取值范围．

Answer 1

【答案】分析：（1）建立空间直角坐标系，用坐标表示向量、，利用向量的夹角公式，可求异面直线AF和BE所成的角的余弦值：
（2）确定平面ACC₁、平面BFC₁的法向量，利用向量的夹角公式，即可求得平面ACC₁与平面BFC₁所成的锐二面角；
（3）用坐标表示出，求出模长，利用配方法，即可求得EP的取值范围．
解答：解：（1）以D为原点，DA，DC，DD₁分别为x，y，z轴，建立如图所示的直角坐标系，
则A（1，0，0），E（，0，1），B（1，1，0），F（1，，1）．
∴=（0，，1），=（-，-1，1），
∴cos==；
（2）平面ACC₁的一个法向量为
设平面BFC₁的法向量为
由，可得，
∴，可取z=1，则
∴cos===
∵为锐角
∴所求的锐二面角为；
（3）设P（x，y，0）（0≤x≤1，0≤y≤1），则
由得，即x=-2y+，
∵0≤x≤1，∴0≤-2y+≤1，∴
∵
∴==
∵，∴当y=时，=；当y=时，=，
故EP的取值范围为[，]．
点评：本题考查向量知识的运用，考查线线角、面面角，考查线段长的取值范围，考查学生的计算能力，用坐标表示向量是关键．