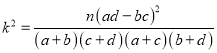题目内容
【题目】已知函数f(x)=(3-x)ex,g(x)=x+a(a∈R)(e是自然对数的底数,e≈2.718…).
(1)求函数f(x)的极值;
(2)若函数y=f(x)g(x)在区间[1,2]上单调递增,求实数a的取值范围;
(3)若函数h(x)=![]() 在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
在区间(0,+∞)上既存在极大值又存在极小值,并且函数h(x)的极大值小于整数b,求b的最小值.
【答案】(1)见解析;(2)![]() ;(3)4
;(3)4
【解析】
(1)对![]() 求导,通过
求导,通过![]() 的正负,列表分析
的正负,列表分析![]() 的单调性进而求得极值.
的单调性进而求得极值.
(2)先求得![]() 的解析式,对其求导,原题转化为导函数
的解析式,对其求导,原题转化为导函数![]() 在
在![]() 上恒成立,令
上恒成立,令![]() ,求得a的范围.(3)由题意知
,求得a的范围.(3)由题意知![]() 在
在![]() 上有两个不等实根,即
上有两个不等实根,即![]() 在
在![]() 上有两个不等实根,对
上有两个不等实根,对![]() 求导分析可得
求导分析可得![]() 在
在![]() 和
和![]() 上各有一个实根,从而得到极大值
上各有一个实根,从而得到极大值![]() ,将
,将![]() 视为关于
视为关于![]() 的函数,求导得到
的函数,求导得到![]() ,又因为
,又因为![]() ,得到整数b的最小值.
,得到整数b的最小值.
(1)![]() ,
,![]() ,令
,令![]() ,解得
,解得![]() ,列表:
,列表:
|
| 2 |
|
| + | 0 | - |
|
| 极大值 |
|
∴当![]() 时,函数
时,函数![]() 取得极大值
取得极大值![]() ,无极小值
,无极小值
(2)由![]() ,得
,得![]()
![]()
∵![]() ,令
,令![]() ,
,
∴函数![]() 在区间
在区间![]() 上单调递增等价于对任意的
上单调递增等价于对任意的![]() ,函数
,函数![]() 恒成立
恒成立
∴![]() ,解得
,解得![]() .
.
(3)![]() ,
,![]()
令![]() ,
,
∵![]() 在
在![]() 上既存在极大值又存在极小值,∴
上既存在极大值又存在极小值,∴![]() 在
在![]() 上有两个不等实根,
上有两个不等实根,
即![]() 在
在![]() 上有两个不等实根
上有两个不等实根![]() .
.
∵![]()
∴当![]() 时,
时,![]() ,
,![]() 单调递增,当
单调递增,当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
则![]() ,∴
,∴![]() ,解得
,解得![]() ,∴
,∴![]()
∵![]() 在
在![]() 上连续且
上连续且![]() ,
,![]()
∴![]() 在
在![]() 和
和![]() 上各有一个实根
上各有一个实根
∴函数![]() 在
在![]() 上既存在极大值又存在极小值时,有
上既存在极大值又存在极小值时,有![]() ,并且在区间
,并且在区间![]() 上存在极小值
上存在极小值![]() ,在区间
,在区间![]() 上存在极大值
上存在极大值![]() .
.
∴![]() ,且
,且![]()
![]() ,
,![]()
![]()
令![]() ,
,![]() ,当
,当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
∵![]() ,∴
,∴![]() ,即
,即![]() ,则
,则![]()
∵![]() 的极大值小于整数
的极大值小于整数![]() ,∴满足题意的整数
,∴满足题意的整数![]() 的最小值为4.
的最小值为4.

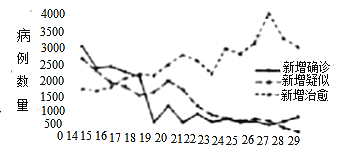
【题目】2018年为我国改革开放40周年,某事业单位共有职工600人,其年龄与人数分布表如下:
年龄段 |
|
|
|
|
人数(单位:人) | 180 | 180 | 160 | 80 |
约定:此单位45岁~59岁为中年人,其余为青年人,现按照分层抽样抽取30人作为全市庆祝晚会的观众.
(1)抽出的青年观众与中年观众分别为多少人?
(2)若所抽取出的青年观众与中年观众中分别有12人和5人不热衷关心民生大事,其余人热衷关心民生大事.完成下列![]() 列联表,并回答能否有
列联表,并回答能否有![]() 的把握认为年龄层与热衷关心民生大事有关?
的把握认为年龄层与热衷关心民生大事有关?
热衷关心民生大事 | 不热衷关心民生大事 | 总计 | |
青年 | 12 | ||
中年 | 5 | ||
总计 | 30 |
(3)若从热衷关心民生大事的青年观众(其中1人擅长歌舞,3人擅长乐器)中,随机抽取2人上表演节目,则抽出的2人能胜任才艺表演的概率是多少?
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
 .
.
【题目】心理学家发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学,给所有同学几何和代数各一题,让各位同学自由选择一道题进行解答,统计情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男 同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)现从选择几何题的8名女生中任意抽取两人对他们的答题进行研究,记甲、乙两名女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |