题目内容
设
=(3，2)，
=(2，4)(0为坐标原点)，点H（m+2，m-1）为△ABC的垂心，则m=
| AB |
| OC |
2
2
．分析：先求出向量
的坐标，然后根据点H（m+2，m-1）为△ABC的垂心，则CH⊥AB，最后利用
•
=0可求出m的值．
| CH |
| CH |
| AB |
解答：解：∵
=(2，4)，
∴C（2，4），又H（m+2，m-1），
∴
=（m，m-5），
∵点H（m+2，m-1）为△ABC的垂心，
∴CH⊥AB，且
=（3，2），
∴
•
=0，
即m×3+（m-5）×2=0，
解得m=2．
故答案为：2．
| OC |
∴C（2，4），又H（m+2，m-1），
∴
| CH |
∵点H（m+2，m-1）为△ABC的垂心，
∴CH⊥AB，且
| AB |
∴
| CH |
| AB |
即m×3+（m-5）×2=0，
解得m=2．
故答案为：2．
点评：本题主要考查了向量在几何中的应用，以及垂心的含义，同时考查了向量数量积的运用，属于基础题．
练习册系列答案
相关题目
，
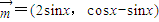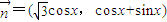，函数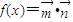
．
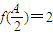且a2=bc，试判断△ABC的形状．
．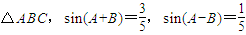