题目内容

已知点A（x1，x12）、B（x2，x22）是函数y=x2的图象上任意不同两点，依据图象可知，线段AB总是位于A、B两点之间函数图象的上方，因此有结论
x
2
1
+
x
2
2
2
＞(
x1+x2
2
)2成立．运用类比思想方法可知，若点A（x1，lgx1）、B（x2，lgx2）是函数y=lgx（x∈R+）的图象上的不同两点，则类似地有
 
成立．
分析：由类比推理的规则得出结论，本题中所用来类比的函数是一个变化率越来越大的函数，而要研究的函数是一个变化率越来越小的函数，其类比方式可知
解答：解：由题意变化率逐渐变大的函数有线段AB总是位于A、B两点之间函数图象的上方，因此有结论
x
2
1
+
x
2
2
2
＞(
x1+x2
2
)2成立
函数y=lgx（x∈R+）变化率逐渐变小，函数有线段AB总是位于A、B两点之间函数图象的下方，故可类比得到结论
lgx1+lgx2
2
＜lg
x1+x2
2

故答案为
lgx1+lgx2
2
＜lg
x1+x2
2
点评：本题考查类比推理，求解本题的关键是理解类比的定义，及本题类比的对象之间的联系与区别，从而得出类比结论
练习册系列答案
相关题目
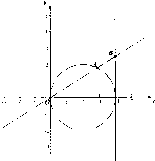精英家教网已知点A（x1，y1）在圆（x-2）2+y2=4上运动，点A不与（0，0）重合，点B（4，y0）在直线x=4上运动，动点M（x，y）满足
OM
∥
OB
，
OM
=
AB
．动点M的轨迹C的方程为F（x，y）=0．
（1）试用点M的坐标x，y表示y0，x1，y1；
（2）求动点M的轨迹方程F（x，y）=0；
（3）以下给出曲线C的五个方面的性质，请你选择其中的三个方面进行研究，并说明理由．（若你研究的方面多于三个，我们将只对试卷解答中的前三项予以评分）
①对称性；
②顶点坐标（定义：曲线与其对称轴的交点称为该曲线的顶点）；
③图形范围；
④渐近线；
⑤对方程F（x，y）=0，当y≥0时，函数y=f（x）的单调性．
已知点A（x1，y1），B（x2，y2）是函数f（x）=sin（ωx+φ）（ω＞0，0＜φ＜
π
2
）图象上的任意两点，若|y1-y2）=2时，|x1-x2|的最小值为
π
2
，且函数f（x）的图象经过点（0，
1
2
）．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）在△ABC中，角A，B，C的对边分别为a，b，c，且2sinAsinC+cos2B=1，求f（B）的取值范围．
（2011•江西模拟）已知函数f（x）=ax-lnx+1（a∈R），g（x）=xe1-x．
（1）求函数g（x）在区间（0，e]上的值域；
（2）是否存在实数a，对任意给定的x0∈（0，e]，在区间[1，e]上都存在两个不同的xi（i=1，2），使得f（xi）=g（x0）成立．若存在，求出a的取值范围；若不存在，请说明理由．
（3）给出如下定义：对于函数y=F（x）图象上任意不同的两点A（x1，y1），B（x2，y2），如果对于函数y=F（x）图象上的点M（x0，y0）（其中x0=
x1+x22
)总能使得F（x1）-F（x2）=F'（x0）（x1-x2）成立，则称函数具备性质“L”，试判断函数f（x）是不是具备性质“L”，并说明理由．
已知点A（x1，x12）、B（x2，x22）是函数y=x2的图象上任意不同两点，依据图象可知，线段AB总是位于A、B两点之间函数图象的上方，因此有结论
x21
+
x22
2
＞(
x1+x2
2
)2成立．运用类比思想方法可知，若点A（x1，lgx1）、B（x2，lgx2）是函数y=lgx（x∈R+）的图象上的不同两点，则类似地有______成立．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网