题目内容
已知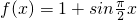 ,则f(1)+f(2)+f(3)+…+f(2009)=________.
,则f(1)+f(2)+f(3)+…+f(2009)=________.
解:由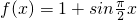 ,
,
则f(1)+f(2)+f(3)+…+f(2009)
=1+sin +1+sinπ+1+sin
+1+sinπ+1+sin +1+sin2π+1+sin
+1+sin2π+1+sin +…+1+sin
+…+1+sin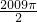
=2009+(sin +sinπ+sin
+sinπ+sin +sin2π)+(sin
+sin2π)+(sin +sin3π+sin
+sin3π+sin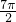 +sin4π)+…+(sin
+sin4π)+…+(sin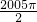 +sin1003π+sin
+sin1003π+sin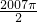 +sin1004π)
+sin1004π)
+sin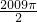 =2009+(sin
=2009+(sin +sinπ+sin
+sinπ+sin +sin2π)+(sin
+sin2π)+(sin +sinπ+sin
+sinπ+sin +sin2π)+…+(sin
+sin2π)+…+(sin +sinπ+sin
+sinπ+sin +sin2π)+sin
+sin2π)+sin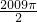
=2009+0+0+…+0+sin(2×502π+ )
)
=2009+1
=2010
故答案为:2010
分析:分别把x=1,2,3,…,2009代入f(x)求出各项,除过2009个1外,根据诱导公式和特殊角的三角函数值可得:从sin 开始每连续的四个正弦值相加为0,因为2009除以4余数是1,所以把最后一项的sin(
开始每连续的四个正弦值相加为0,因为2009除以4余数是1,所以把最后一项的sin(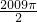 )利用诱导公式求出值即可得到原式的值.
)利用诱导公式求出值即可得到原式的值.
点评:此题是一道基础题,要求学生灵活运用诱导公式化简求值,牢记特殊角的三角函数值.做题时要找出每四项的正弦值为0这个规律.
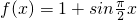 ,
,则f(1)+f(2)+f(3)+…+f(2009)
=1+sin
 +1+sinπ+1+sin
+1+sinπ+1+sin +1+sin2π+1+sin
+1+sin2π+1+sin +…+1+sin
+…+1+sin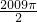
=2009+(sin
 +sinπ+sin
+sinπ+sin +sin2π)+(sin
+sin2π)+(sin +sin3π+sin
+sin3π+sin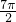 +sin4π)+…+(sin
+sin4π)+…+(sin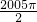 +sin1003π+sin
+sin1003π+sin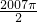 +sin1004π)
+sin1004π)+sin
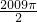 =2009+(sin
=2009+(sin +sinπ+sin
+sinπ+sin +sin2π)+(sin
+sin2π)+(sin +sinπ+sin
+sinπ+sin +sin2π)+…+(sin
+sin2π)+…+(sin +sinπ+sin
+sinπ+sin +sin2π)+sin
+sin2π)+sin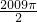
=2009+0+0+…+0+sin(2×502π+
 )
)=2009+1
=2010
故答案为:2010
分析:分别把x=1,2,3,…,2009代入f(x)求出各项,除过2009个1外,根据诱导公式和特殊角的三角函数值可得:从sin
 开始每连续的四个正弦值相加为0,因为2009除以4余数是1,所以把最后一项的sin(
开始每连续的四个正弦值相加为0,因为2009除以4余数是1,所以把最后一项的sin(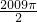 )利用诱导公式求出值即可得到原式的值.
)利用诱导公式求出值即可得到原式的值.点评:此题是一道基础题,要求学生灵活运用诱导公式化简求值,牢记特殊角的三角函数值.做题时要找出每四项的正弦值为0这个规律.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
 ,则f(1)+f(2)+…+f(2011)+f(2012)=( )
,则f(1)+f(2)+…+f(2011)+f(2012)=( )

 ,则f(1)+f(2)+f(3)+…+f(2010)= .
,则f(1)+f(2)+f(3)+…+f(2010)= .