题目内容
已知 ,则f(1)+f(2)+f(3)+…+f(2010)= .
,则f(1)+f(2)+f(3)+…+f(2010)= .
【答案】分析:把函数解析式中n换为n+6,变形后利用诱导公式sin(2π+α)=cosα进行化简,得到f(n+8)=f(n),即函数周期是8,把所求的式子中括号去掉后,重新结合,根据函数的周期化简,即可求出值.
解答:解:∵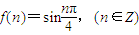 ,
,
∴f(n+8)=sin(2π+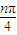 )=sin
)=sin =f(n),
=f(n),
∴f(1)+f(2)+f(3)+…+f(2010)
=251×(sin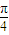 +sin
+sin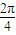 +sin
+sin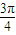 +sin
+sin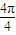 +sin
+sin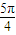 +sin
+sin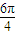 +sin
+sin +sin
+sin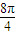 )+sin
)+sin +sin
+sin
=251×(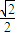 +1+
+1+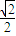 +0-
+0-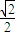 -1-
-1-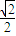 +0)+sin
+0)+sin +sin
+sin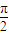
=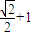 .
.
故答案为: .
.
点评:此题考查了三角函数的周期性及其求法,其中根据题意利用了诱导公式得出f(n+8)=f(n)是解本题的关键.
解答:解:∵
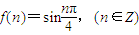 ,
,∴f(n+8)=sin(2π+
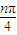 )=sin
)=sin =f(n),
=f(n),∴f(1)+f(2)+f(3)+…+f(2010)
=251×(sin
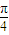 +sin
+sin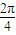 +sin
+sin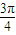 +sin
+sin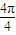 +sin
+sin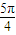 +sin
+sin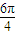 +sin
+sin +sin
+sin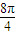 )+sin
)+sin +sin
+sin
=251×(
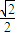 +1+
+1+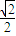 +0-
+0-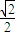 -1-
-1-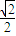 +0)+sin
+0)+sin +sin
+sin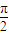
=
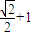 .
.故答案为:
 .
.点评:此题考查了三角函数的周期性及其求法,其中根据题意利用了诱导公式得出f(n+8)=f(n)是解本题的关键.

练习册系列答案
相关题目
 ,则f(1)+f(2)+…+f(2011)+f(2012)=( )
,则f(1)+f(2)+…+f(2011)+f(2012)=( )
