题目内容
如图3,已知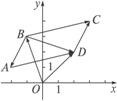
图3
活动:本例的目的仍然是让学生熟悉平面向量的坐标运算.这里给出了两种解法:解法一利用“两个向量相等,则它们的坐标相等”,解题过程中应用了方程思想;解法二利用向量加法的平行四边形法则求得向量![]() 的坐标,进而得到点D的坐标.解题过程中,关键是充分利用图形中各线段的位置关系(主要是平行关系),数形结合地思考,将顶点D的坐标表示为已知点的坐标.
的坐标,进而得到点D的坐标.解题过程中,关键是充分利用图形中各线段的位置关系(主要是平行关系),数形结合地思考,将顶点D的坐标表示为已知点的坐标.
解:方法一:如图3,设顶点D的坐标为(x,y).
∵![]() =(-1-(-2),3-1)=(1,2),
=(-1-(-2),3-1)=(1,2),![]() =(3-x,4-y).
=(3-x,4-y).
由![]() =
=![]() ,得(1,2)=(3-x,4-y).
,得(1,2)=(3-x,4-y).
∴![]()
∴![]()
∴顶点D的坐标为(2,2).
方法二:如图3,由向量加法的平行四边形法则,可知
![]() =
=![]() +
+![]() =
=![]() +
+![]() =(-2-(-1),1-3)+(3-(-1),4-3)=(3,-1),
=(-2-(-1),1-3)+(3-(-1),4-3)=(3,-1),
而![]() =
=![]() +
+![]() =(-1,3)+(3,-1)=(2,2),
=(-1,3)+(3,-1)=(2,2),
∴顶点D的坐标为(2,2).
点评:本例的目的仍然是让学生熟悉平面向量的坐标运算.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
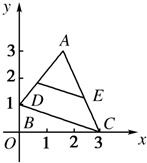 如图,已知A(2,3),B(0,1),C(3,0),点D,E分别在AB,AC上,DE∥BC,且DE平分△ABC的面积,求点D的坐标.
如图,已知A(2,3),B(0,1),C(3,0),点D,E分别在AB,AC上,DE∥BC,且DE平分△ABC的面积,求点D的坐标.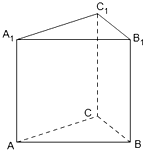 如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.
如图,已知A,B,C为不在同一直线上的三点,且AA1∥BB1∥CC1,AA1=BB1=CC1.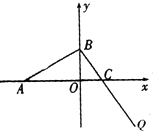 如图,已知A(-3,0),B、C两点分别在y轴和x轴上运动,并且满足
如图,已知A(-3,0),B、C两点分别在y轴和x轴上运动,并且满足
