题目内容
如图,已知A、B、C是直线m上的三点,且|AB|=|BC|=6,⊙O′切直线m于点A,又过B、C作⊙O′异于m的两切线,切点分别为D、E,设两切线交于点P,
(1)求点P的轨迹方程;
(2)经过点C的直线l与点P的轨迹交于M、N两点,且点C分![]() 所成比等于2∶3,求直线l的方程.
所成比等于2∶3,求直线l的方程.
解:(1)∵|PE|=|PD|,|BD|=|BA|,|CE|=|CA|,
∴|PB|+|PC|=|PD|+|DB|+|CE|-|PE|=|BD|+|CE|=|AB|+|CA|=18>6=|BC|.
∴P点轨迹是以B、C为焦点,长轴长等于18的椭圆.故可以B、C两点所在直线为x轴,线段BC的垂直平分线为y轴建立平面直角坐标系,设椭圆的方程是![]() +
+![]() =1(a>b>0).
=1(a>b>0).
∵a=9,c=3,∴b2=72.
∴P点的轨迹方程是![]() =1(y≠0).
=1(y≠0).
(2)设M(x1,y1)、N(x2,y2),∵C(3,0)分MN所成的比为![]() ,则有
,则有
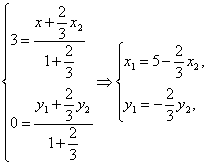
又∵![]() =1,
=1,
∴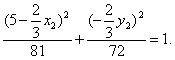 ①
①
又![]() =1, ②
=1, ②
由①②消去y2:![]() (5-
(5-![]() x2)2+
x2)2+![]() (1-
(1-![]() )=1,解得x2=-3,y2=±8,即N(-3,±8).
)=1,解得x2=-3,y2=±8,即N(-3,±8).
∴由C、N可得直线l的方程是4x+3y-12=0或4x-3y-12=0.

练习册系列答案
相关题目
 17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|=
17、如图,已知A、B、C、D分别为过抛物线y2=4x焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|= 如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( )
如图,已知A、B、C、D分别为过抛物线y2=4x的焦点F的直线与该抛物线和圆(x-1)2+y2=1的交点,则|AB|•|CD|等于( ) 如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC.
如图,已知A、B、C、D四点共圆,延长AD和BC相交于点E,AB=AC. 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且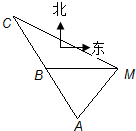 (2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )
(2009•台州二模)如图,已知A、B、C是一条直路上的三点,一个人从A出发行走到B处时,望见塔M(将塔M视为与A、B、C在同一水平面上一点)在正东方向且A在东偏南α方向,继续行走1km在到达C处时,望见塔M在东偏南β方向,则塔M到直路ABC的最短距离为( )