题目内容

方程：cos2x+2sinxcosx=-1的解集是________．


分析：由已知-1=cos2x+2sinxcosx=cos2x+sin2x═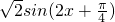可得，解三角方程可求
解答：∵-1=cos2x+2sinxcosx=cos2x+sin2x═
∴
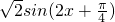
∴或
∴x=或，k∈Z
故答案为：x=或，k∈Z
点评：本题主要考查了二倍角公式、辅助角公式在三角函数化简中的应用，及由特殊的 三角函数值求解角．
练习册系列答案
相关题目
已知函数f(x)=sin(2x+
π
6
)+sin(2x-
π
6
)-cos2x+a(a∈R)
（1）求函数f（x）的最小正周期和图象的对称轴方程；
（2）若x∈[0，
π
2
]时，f（x）的最小值为-2，求a的值．
方程：cos2x+2sinxcosx=-1的解集是
{x|x=kπ+
π
2
，x=kπ-
π
4
(k∈Z)}
{x|x=kπ+
π
2
，x=kπ-
π
4
(k∈Z)}
．
（1）解方程：log2（9x-5）=log2（3x-2）+2；
（2）已知：0≤x＜2π，解方程：cos2x=cosx（sinx+|sinx|）．
方程sinx=cos2x的解集是
{x|x=nπ+(-1)n
π
6
或x=2nπ-
π
2
，n∈Z}
{x|x=nπ+(-1)n
π
6
或x=2nπ-
π
2
，n∈Z}
．
设函数f(x)=
a
•
b
，其中向量
a
=(1，cos2x)，
b
=(1+sin2x，
3
)，x∈R，
（1）求函数f（x）的单调递减区间及对称轴方程；
（2）求使f（x）≥0成立的x的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网