题目内容
14.在等比数列{an}中,已知对任意正整数n,a1+a2+…+an=3n-1,则a12+a22+…+an2=$\frac{{9}^{n}-1}{2}$.分析 由an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$能求出${a}_{n}=2•{3}^{n-1}$,从而得到${{a}_{n}}^{2}=4•{9}^{n-1}$,由此能求出a12+a22+…+an2的值.
解答 解:∵在等比数列{an}中,a1+a2+…+an=3n-1,
∴a1=3-1=2,
an=Sn-Sn-1=(3n-1)-(3n-1-1)=$\frac{2}{3}•{3}^{n}$=2•3n-1,
∴${{a}_{n}}^{2}=4•{9}^{n-1}$,
∴a12+a22+…+an2=4×(1+9+92+…+9n-1)
=4×$\frac{1-{9}^{n}}{1-9}$
=$\frac{{9}^{n}-1}{2}$.
故答案为:$\frac{{9}^{n}-1}{2}$.
点评 本题考查等比数列的各项的平方的和的求法,是中档题,解题时要注意等比数列的性质和公式an=$\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$的合理运用.

练习册系列答案
相关题目
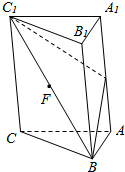 如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC.
如图,在正棱柱ABC-A1B1C1中,E,F分别为线段AA1,C1B的中点,求证:EF∥平面ABC.