题目内容
设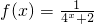 ,利用课本中推导等差数列前n项和的公式的方法,可求得f(-3)+f(-2)+…+f(0)+…+f(3)+f(4)的值为________.
,利用课本中推导等差数列前n项和的公式的方法,可求得f(-3)+f(-2)+…+f(0)+…+f(3)+f(4)的值为________.
2
分析:先考察函数f(x)具有的性质:若a+b=1,则f(a)+f(b)= ,由此可求答案.
,由此可求答案.
解答:设a+b=1,则f(a)+f(b)= +
+
= +
+ =
= +
+ =
= =
= .
.
所以f(-3)+f(4)= ,f(-2)+f(3)=
,f(-2)+f(3)= ,f(-1)+f(2)=
,f(-1)+f(2)= ,f(0)+f(1)=
,f(0)+f(1)= ,
,
f(-3)+f(-2)+…+f(0)+…+f(3)+f(4)=4× =2.
=2.
故答案为:2.
点评:本题考查根据数列是特殊的函数,根据函数具有的性质,来解决数列的和问题,利用的是倒序相加法,属于基础题.
分析:先考察函数f(x)具有的性质:若a+b=1,则f(a)+f(b)=
 ,由此可求答案.
,由此可求答案.解答:设a+b=1,则f(a)+f(b)=
 +
+
=
 +
+ =
= +
+ =
= =
= .
.所以f(-3)+f(4)=
 ,f(-2)+f(3)=
,f(-2)+f(3)= ,f(-1)+f(2)=
,f(-1)+f(2)= ,f(0)+f(1)=
,f(0)+f(1)= ,
,f(-3)+f(-2)+…+f(0)+…+f(3)+f(4)=4×
 =2.
=2.故答案为:2.
点评:本题考查根据数列是特殊的函数,根据函数具有的性质,来解决数列的和问题,利用的是倒序相加法,属于基础题.

练习册系列答案
相关题目
 ,利用课本中推导等差数列前n项和公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值是______
,利用课本中推导等差数列前n项和公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值是______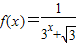 ,利用课本中推导等差数列前n项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为( )
,利用课本中推导等差数列前n项和公式的方法,可求得f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为( )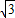
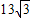
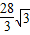
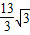
 ,利用课本中推导等差数列前n项和的公式的方法,可求得:f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为 .
,利用课本中推导等差数列前n项和的公式的方法,可求得:f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为 . ,利用课本中推导等差数列前n项和的公式的方法,可求得:f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为 .
,利用课本中推导等差数列前n项和的公式的方法,可求得:f(-12)+f(-11)+f(-10)+…+f(0)+…+f(11)+f(12)+f(13)的值为 .