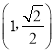题目内容
【题目】已知![]() ,
,![]() 是椭圆
是椭圆![]() :
:![]() 上的两点,线段
上的两点,线段![]() 的中点在直线
的中点在直线![]() 上.
上.
(1)当直线![]() 的斜率
的斜率![]() 存在时,求实数
存在时,求实数![]() 的取值范围;
的取值范围;
(2)设![]() 是椭圆
是椭圆![]() 的左焦点,若椭圆
的左焦点,若椭圆![]() 上存在一点
上存在一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
【答案】(1) ;(2)
;(2)![]()
【解析】
(1)设中点![]() ,利用点差法得
,利用点差法得![]() ,由点在椭圆内部得
,由点在椭圆内部得![]() ,即可求解k的范围
,即可求解k的范围
(2)向量坐标化得![]() ,
,![]() ,弦长公式得
,弦长公式得![]() 由点
由点![]() 在椭圆上,得
在椭圆上,得![]() ,进而得AB方程,与椭圆联立得
,进而得AB方程,与椭圆联立得![]() ,则可求
,则可求![]()
(1)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
两式相减得:![]()
![]() ,
,
由线段![]() 的中点在直线
的中点在直线![]() 上,可设此中点
上,可设此中点![]() ,因为直线
,因为直线![]() 的斜率存在,所以
的斜率存在,所以![]() ,
,
设其斜率为![]() ,由
,由![]() 式得
式得![]() ,即
,即![]() .
.
由于弦![]() 的中点
的中点![]() 必在椭圆内部,则
必在椭圆内部,则![]() ,解得
,解得![]() .
.
又![]() ,所以斜率
,所以斜率![]() 的取值范围为
的取值范围为 .
.
(2)由(1)知![]() ,
,![]() ,因为椭圆的左焦点
,因为椭圆的左焦点![]() 为
为![]() ,
,
所以![]() ,
,![]() ,设
,设![]() ,则
,则![]() ,
,
![]()
![]() ,
,![]() ,
,
![]() ,
,
同理可得![]() ,因为点
,因为点![]() 在椭圆上,所以
在椭圆上,所以![]() ,
,
解得![]() .当
.当![]() 时,
时,![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
代入![]() 得
得![]() ,由根与系数关系得
,由根与系数关系得![]() .
.
则![]()
![]() .
.
由对称性知,当![]() 时
时![]() 也成立,
也成立,![]() .
.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目