题目内容
16．设x1，x2是关于x的一元二次方程x2-2（m-1）x+m+5=0的两个实根，又y=x21+x22，求y=f（m）的解析式及此函数的定义域．分析 利用韦达定理转化求解函数的解析式，求解函数的定义域．
解答 解：∵x1，x2是x2-2（m-1）x+m+5=0的两个实根，
∴△=4（m-1）2-4（m+5）≥0，解得m≤-1或m≥4．------------（4分）
又∵x1+x2=2（m-1），x1•x2=m+5，------------（6分）
∴y=f（m）=x12+x22=（x1+x2）2-2x1x2=4m2-10m-6，------（10分）
即y=f（m）=4m2-10m-6 （m≤-1或m≥4）．--------（12分）
点评 本题考查函数的解析式的求法，考查计算能力．
练习册系列答案
相关题目
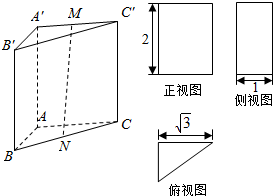已知一个三棱柱ABC-A′B′C′的三视图由一个直角三角形和两个矩形组成，如图若M，N分别是A′C′，BC的中点．
1．若函数y=log${\;}_{\frac{1}{2}}$（3x2-6x十5）在[a，+∞）上是减函数，则实数a的取值范围是（ ）
| A． | [1，+∞） | B． | [2，+∞） | C． | （-∞，2] | D． | （-∞，1] |