题目内容
【题目】已知抛物线![]() :
:![]() (
(![]() ),圆
),圆![]() :
:![]() (
(![]() ),抛物线
),抛物线![]() 上的点到其准线的距离的最小值为
上的点到其准线的距离的最小值为![]() .
.
(1)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
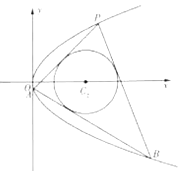
(2)如图,点![]() 是抛物线
是抛物线![]() 在第一象限内一点,过点P作圆
在第一象限内一点,过点P作圆![]() 的两条切线分别交抛物线
的两条切线分别交抛物线![]() 于点A,B(A,B异于点P),问是否存在圆
于点A,B(A,B异于点P),问是否存在圆![]() 使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
使AB恰为其切线?若存在,求出r的值;若不存在,说明理由.
【答案】(1)![]() 的方程为
的方程为![]() ,准线方程为
,准线方程为![]() .(2)存在,
.(2)存在,![]()
【解析】
(1)由![]() 得到p即可;
得到p即可;
(2)设![]() ,利用点斜式得到PA的的方程为
,利用点斜式得到PA的的方程为![]() ,由
,由![]() 到PA的距离为半径可得
到PA的距离为半径可得![]() ,同理
,同理![]() ,同理写出直线AB的方程,利用点
,同理写出直线AB的方程,利用点![]() 到直线AB的距离为半径建立方程即可.
到直线AB的距离为半径建立方程即可.
解:(1)由题意得![]() ,解得
,解得![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() ,准线方程为
,准线方程为![]() .
.
(2)由(1)知,![]() .
.
假设存在圆![]() 使得AB恰为其切线,设
使得AB恰为其切线,设![]() ,
,![]() ,
,
则直线PA的的方程为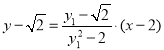 ,即
,即![]() .
.
由点![]() 到PA的距离为r,得
到PA的距离为r,得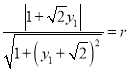 ,
,
化简,得![]() ,
,
同理,得![]() .
.
所以![]() ,
,![]() 是方程的
是方程的![]() 两个不等实根,
两个不等实根,
故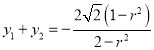 ,
,![]() .
.
易得直线AB的方程为![]() ,
,
由点![]() 到直线AB的距离为r,得
到直线AB的距离为r,得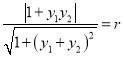 ,
,
所以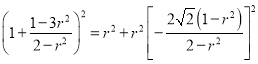 ,
,
于是,![]() ,
,
化简,得![]() ,即
,即![]() .
.
经分析知,![]() ,因此
,因此![]() .
.

练习册系列答案
相关题目