题目内容
已知M={x|（x-1）（x+2）（x+1）＞0}，N={x|x2+px+q≤0}，若M∪N=（-2，+∞），M∩N=（1，3]，则p=______，q=______；
∵M={x|（x-1）（x+2）（x+1）＞0}
={x|x＞1或-2＜x＜-1}，
又∵M∪N=（-2，+∞），M∩N=（1，3]，
∴N={-1，3]，
又N={x|x2+px+q≤0}，
∴方程x2+px+q=0的两个根是：-1，3
∴
∴
故答案为：-2；-3．
={x|x＞1或-2＜x＜-1}，
又∵M∪N=（-2，+∞），M∩N=（1，3]，
∴N={-1，3]，
又N={x|x2+px+q≤0}，
∴方程x2+px+q=0的两个根是：-1，3
∴
|
∴
|
故答案为：-2；-3．
练习册系列答案
相关题目
已知M={x|y=
}，N={y|y=x2+2x+1}，则M∩N=（ ）
| x2-1 |
| A、{x|x≥0} |
| B、{x|x≤-1} |
| C、{x|x≥1} |
| D、φ |
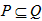，求实数a的取值范围.