题目内容
(本小题满分l2分)
已知函数
．
(I) 设
求函数
的单调区间；
(Ⅱ) 设
若方程=0在[-2，2]上有且仅有一个实数解，求
的取值范围．
（本小题满分12分）
解：（I）
，………………2分
因为
，所以
当
变化时，
，
的变化情况如下表：
当
或
时，
；
当
时，
.
所以，当时，函数的单调递增区间是
和
，
单调递减区间是
．……………………6分
（II）
，
，
当变化时，，的变化情况如下表：
|
|
|
| 0 |
| 2 |
|
| － | 0 | ＋ | ||
|
|
| 递减 | 极小值 | 递增 |
|
…………………8分
因为方程
在区间
有且仅有一个实数解，而
，
所以
，…………………10分
或
所以方程在区间有且仅有一个实数解时，
的取值范围是或
.……………………12分
练习册系列答案
全能测控期末小状元系列答案
相关题目
，bn＋1＝－
Sn（n∈N*）．
＋
＋…＋
，求Tn的表达式
，过左焦点
作直线
与椭圆交于点P，Q，直线AP，AQ分别与直线
交于点
．
为直径的圆经过焦点
．
：函数
（
）的值域是
；命题
：指数函数
在
上是减函数．若命题“
的范围．
并且与曲线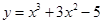
相切的直线方程.