题目内容
在△ABC中,若cosBcosC-sinBsinC≥0,则这个三角形一定不是
- A.钝角三角形
- B.直角三角形
- C.锐角三角形
- D.以上都有可能
C
分析:由题意利用两角和的余弦公式可得 cos(B+C)≥0,故B+C为锐角或直角,故角A为钝角或直角,从而可得此三角形为钝角三角形或直角三角形,由此得出结论.
解答:在△ABC中,若cosBcosC-sinBsinC≥0,则有 cos(B+C)≥0,故B+C为锐角或直角,故角A为钝角或直角,
从而可得此三角形为钝角三角形或直角三角形,故一定不是锐角三角形,
故选C.
点评:本题主要考查两角和的余弦公式,判断三角形的形状的方法,属于中档题.
分析:由题意利用两角和的余弦公式可得 cos(B+C)≥0,故B+C为锐角或直角,故角A为钝角或直角,从而可得此三角形为钝角三角形或直角三角形,由此得出结论.
解答:在△ABC中,若cosBcosC-sinBsinC≥0,则有 cos(B+C)≥0,故B+C为锐角或直角,故角A为钝角或直角,
从而可得此三角形为钝角三角形或直角三角形,故一定不是锐角三角形,
故选C.
点评:本题主要考查两角和的余弦公式,判断三角形的形状的方法,属于中档题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
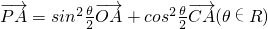 ,则
,则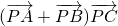 的最小值是________.
的最小值是________.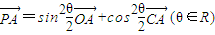 ,则
,则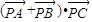 的最小值是 .
的最小值是 .