Question

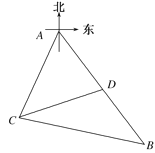
【题目】某观测站在目标的南偏西方向，从出发有一条南偏东走向的公路，在处测得与相距的公路处有一个人正沿着此公路向走去，走到达，此时测得距离为，若此人必须在分钟内从处到达处，则此人的最小速度为(　　)

A. B. C. D.

Answer 1

【答案】B

【解析】由已知得∠CAB＝25°＋35°＝60°，BC＝31，CD＝21，BD＝20，可得，那么，

于是在△ABC中， ＝24，

在△ABC中，BC2＝AC2＋AB2－2AC·ABcos60°，即312＝242＋AB2－24AB，解得AB＝35或AB＝－11(舍去)，因此AD＝AB－BD＝35－20＝15.

故此人在D处距A处还有15 km，若此人必须在20分钟，即小时内从D处到达A处，则其最小速度为15÷＝45(km/h)．

故选B.