题目内容
已知数列
是等差数列， 
；数列
的前n项和是
，且
．
(Ⅰ) 求数列的通项公式；
(Ⅱ) 求证：数列是等比数列；
(Ⅲ) 记
，求
的前n项和
．
(Ⅰ)
(Ⅱ)略(Ⅲ) 
解析:
Ⅰ)设
的公差为
，则：
，
，
∵
，
，∴
，∴
．
∴
．
（Ⅱ）当
时，
，由
，得
．
当
时，
，
，
∴
，即
．
∴
．
∴
是以
为首项，
为公比的等比数列．
（Ⅲ）由（2）可知：
．
∴
．
．
∴
．
∴
．
∴．
练习册系列答案
相关题目
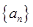是等差数列，若
,
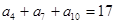，且
,则
_________．
是等差数列，
，则首项
．
是等差数列,
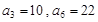，数列
的前n项和是
，且
.
是等差数列，数列
是等比数列，则
的值为 .
}是等差数列，且满足：a1＋a2＋a3＝6，a5＝5；
}满足：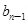
＝
（n≥2，n∈N﹡），b1＝1．
＝
（n∈N﹡），若{
，求