题目内容
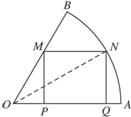
如图所示,在半径为 ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上.设矩形PNMQ的面积为y,∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上.设矩形PNMQ的面积为y,∠POB=θ,将y表示成θ的函数关系式,并求出y的最大值.
【答案】分析:利用三角函数的关系,求出矩形的邻边,求出面积的表达式,化为一个角的一个三角函数的形式,根据θ的范围确定矩形面积的最大值.
解答:解:由题意,PN=OP•sinθ= ,ON=OPcosθ=
,ON=OPcosθ= cosθ,OM=
cosθ,OM= =sinθ
=sinθ
∴MN=ON-OM= cosθ-sinθ
cosθ-sinθ
∴y= sinθ(
sinθ( cosθ-sinθ),
cosθ-sinθ),
即y=3sinθcosθ- sin2θ,θ∈(0,
sin2θ,θ∈(0, )
)
∴y= sin(
sin( )-
)-
∵θ∈(0, )
)
∴
∴sin( )∈
)∈
∴ ,即
,即 时,y的最大值为
时,y的最大值为 .
.
点评:本题考查三角函数模型的建立,考查三角函数的最值,考查学生分析解决问题的能力,属于中档题.
解答:解:由题意,PN=OP•sinθ=
 ,ON=OPcosθ=
,ON=OPcosθ= cosθ,OM=
cosθ,OM= =sinθ
=sinθ∴MN=ON-OM=
 cosθ-sinθ
cosθ-sinθ∴y=
 sinθ(
sinθ( cosθ-sinθ),
cosθ-sinθ),即y=3sinθcosθ-
 sin2θ,θ∈(0,
sin2θ,θ∈(0, )
)∴y=
 sin(
sin( )-
)-
∵θ∈(0,
 )
)∴

∴sin(
 )∈
)∈
∴
 ,即
,即 时,y的最大值为
时,y的最大值为 .
.点评:本题考查三角函数模型的建立,考查三角函数的最值,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图所示,在半径为
如图所示,在半径为
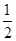 的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.
的正方形ABCD,向半圆内任投一点,则点落在正方形内的概率为________.