题目内容

如图所示，在半径为
3
，圆心角为60°的扇形的弧上任取一点P，作扇形的内接矩形PNMQ，使点Q在OA上，点N，M在OB上．设矩形PNMQ的面积为y，∠POB=θ，将y表示成θ的函数关系式，并求出y的最大值．
分析：利用三角函数的关系，求出矩形的邻边，求出面积的表达式，化为一个角的一个三角函数的形式，根据θ的范围确定矩形面积的最大值．
解答：解：由题意，PN=OP•sinθ=
3
sinθ，ON=OPcosθ=
3
cosθ，OM=
QM
tan60°
=
PN
tan60°
=sinθ
∴MN=ON-OM=
3
cosθ-sinθ
∴y=
3
sinθ（
3
cosθ-sinθ），
即y=3sinθcosθ-
3
sin2θ，θ∈（0，
π
3
）
∴y=
3
sin（2θ+
π
6
）-
3
2

∵θ∈（0，
π
3
）
∴2θ+
π
6
∈(
π
6
，
5π
6
)
∴sin（2θ+
π
6
）∈(
1
2
，1]
∴2θ+
π
6
=
π
2
，即θ=
π
6
时，y的最大值为
3
2
．
点评：本题考查三角函数模型的建立，考查三角函数的最值，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
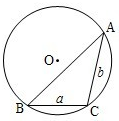精英家教网通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
（1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长；
（2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2；
（3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c．

如图所示，在墙上挂着一块边长为16cm的正方形木板，上面画了小、中、大三个同心圆，半径分别为2cm、4cm、6cm，某人站在3m之外向此板投镖．设投镖击中线上或没有投中木板时都不算，可重投，问：

(1)投中大圆内的概率是多少？

(2)投中小圆与中圆形成的圆环的概率是多少？

(3)投中大圆之外的概率是多少？

通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
（1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长；
（2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2；
（3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c．
通常用a、b、c表示△ABC的三个内角∠A、∠B、∠C所对边的边长，R表示△ABC外接圆半径．
（1）如图所示，在以O为圆心，半径为2的⊙O中，BC和BA是⊙O的弦，其中BC=2，∠ABC=45°，求弦AB的长；
（2）在△ABC中，若∠C是钝角，求证：a2+b2＜4R2；
（3）给定三个正实数a、b、R，其中b≤a，问：a、b、R满足怎样的关系时，以a、b为边长，R为外接圆半径的△ABC不存在，存在一个或两个（全等的三角形算作同一个）？在△ABC存在的情况下，用a、b、R表示c．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网