题目内容
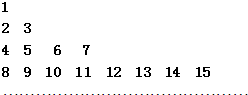 把所有正整数按从小到大的顺序排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数,若aij=2012,则i与j的和为________.
把所有正整数按从小到大的顺序排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数,若aij=2012,则i与j的和为________.
1000
分析:由题目中图中数的排列规律,我们发现图中是把正整数按从小下大、左小右大的原则进行排列,每行的个数成等比数列,每行又构成等差数列,由此推断2012的位置,求得i+j.
解答:(1)数表中前n行共有1+2+22+…+2 n-1=2n-1个数,
即第i行的第一个数是2i-1,
∴aij=2i-1+j-1.
∵210<2012<211,aij=2012,
∴i=11.
令210+j-1=2012,
解得j=2010-210+1=989.i+j=11+989=1000
故答案为:1000
点评:本题考查数阵形式的归纳推理,关键在于得出数的排列规律,准确应用等比数列,等差数列的通项公式.
分析:由题目中图中数的排列规律,我们发现图中是把正整数按从小下大、左小右大的原则进行排列,每行的个数成等比数列,每行又构成等差数列,由此推断2012的位置,求得i+j.
解答:(1)数表中前n行共有1+2+22+…+2 n-1=2n-1个数,
即第i行的第一个数是2i-1,
∴aij=2i-1+j-1.
∵210<2012<211,aij=2012,
∴i=11.
令210+j-1=2012,
解得j=2010-210+1=989.i+j=11+989=1000
故答案为:1000
点评:本题考查数阵形式的归纳推理,关键在于得出数的排列规律,准确应用等比数列,等差数列的通项公式.

练习册系列答案
相关题目
 把所有正整数按从小到大的顺序排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数,若aij=2012,则i与j的和为
把所有正整数按从小到大的顺序排成如图所示的数表,其中第i行共有2i-1个正整数,设aij(i,j∈N*)表示位于这个数表中从上往下数第i行,从左往右数第j个数,若aij=2012,则i与j的和为
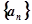 ,若
,若 ,则
,则 .
.
