题目内容
函数y=xcosx+sinx的图象大致为（ ）A．
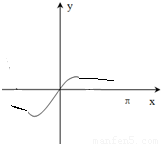
B．
C．
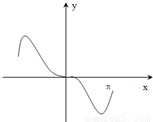
D．
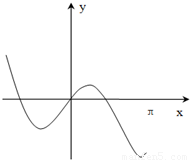
【答案】分析：给出的函数是奇函数，奇函数图象关于原点中心对称，由此排除B，然后利用区特值排除A和C，则答案可求．
解答：解：因为函数y=xcosx+sinx为奇函数，所以排除选项B，
由当x=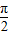
时，
，
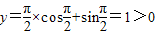当x=π时，y=π×cosπ+sinπ=-π＜0．
由此可排除选项A和选项C．
故正确的选项为D．
故选D．
点评：本题考查了函数的图象，考查了函数的性质，考查了函数的值，是基础题．
解答：解：因为函数y=xcosx+sinx为奇函数，所以排除选项B，
由当x=
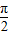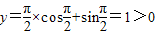时，，当x=π时，y=π×cosπ+sinπ=-π＜0．
由此可排除选项A和选项C．
故正确的选项为D．
故选D．
点评：本题考查了函数的图象，考查了函数的性质，考查了函数的值，是基础题．
练习册系列答案
名校课堂系列答案
相关题目
函数y=-xcosx的部分图象是（ ）
A、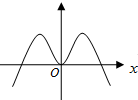 | B、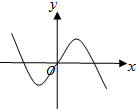 | C、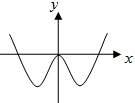 | D、 |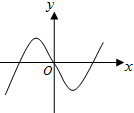
函数y=xcosx-sinx在下面哪个区间内是增函数（ ）
A、（
| ||||
| B、（π，2π） | ||||
C、（
| ||||
| D、（2π，3π） |