题目内容
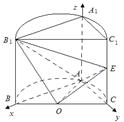
如图4,已知平面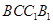 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线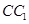 的中点,已知
的中点,已知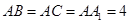
(I))求证: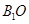 ⊥平面
⊥平面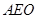 ;
;
(II)求二面角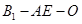 的余弦值.
的余弦值.
(Ⅲ)求三棱锥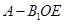 的体积.
的体积. 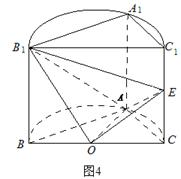
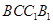 是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线
是圆柱的轴截面(经过圆柱的轴的截面),BC是圆柱底面的直径,O为底面圆心,E为母线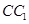 的中点,已知
的中点,已知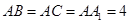
(I))求证:
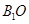 ⊥平面
⊥平面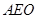 ;
;(II)求二面角
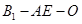 的余弦值.
的余弦值.(Ⅲ)求三棱锥
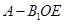 的体积.
的体积. 
(I))见解析(II)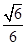 (Ⅲ)8
(Ⅲ)8
 (Ⅲ)8
(Ⅲ)8解:依题意可知, 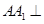 平面ABC,∠
平面ABC,∠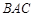 =90°,
=90°,
方法1:空间向量法 如图建立空间直角坐标系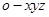 ,
,
因为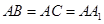 =4,
=4,
则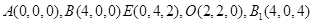
(I)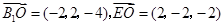 ,
,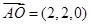
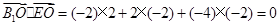 ,∴
,∴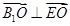 ,∴
,∴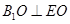
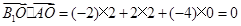 , ∴
, ∴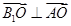 ,∴
,∴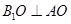
∵
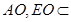 平面
平面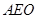 ∴
∴ 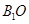 ⊥平面
⊥平面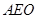 (5分)
(5分)
(II) 平面AEO的法向量为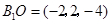 ,设平面 B1AE的法向量为
,设平面 B1AE的法向量为
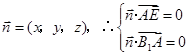 , 即
, 即
令x=2,则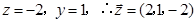
∴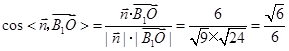
∴二面角B1—AE—F的余弦值为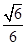 (10分)
(10分)
(Ⅲ)因为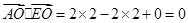 ,∴
,∴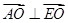 , ∴
, ∴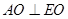
∵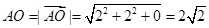 ,
,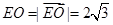
∴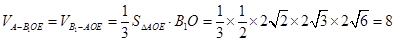 (14 分)
(14 分)
方法2:
依题意可知,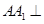 平面ABC,∠
平面ABC,∠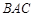 =90°,
=90°,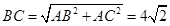 ,∴
,∴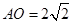
(I)∵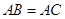 ,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
因为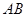 =
=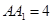 ,则
,则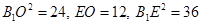 ,∴
,∴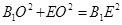
∴B1O⊥EO,∴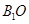 ⊥平面
⊥平面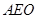 ; (5分)
; (5分)
(II)过O做OM⊥AE于点M,连接B1M,
∵B1O⊥平面AEO,可证B1M⊥AE,
∴∠B1MO为二面角B1—AE—O的平面角,
C1C⊥平面ABC,AO⊥OC,可证EO⊥AO,
在Rt△AEO中,可求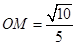 ,
,
在Rt△B1OM中,∠B1OM=90°,∴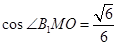
∴二面角B1—AE—O的余弦值为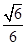 (10分)
(10分)
(Ⅲ)因为AB=AC,O为BC的中点,所以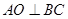
又平面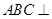 平面
平面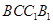 ,且平面
,且平面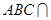 平面
平面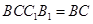 ,
,
所以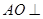 平面
平面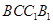 , 故
, 故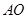 是三棱锥
是三棱锥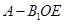 的高
的高
∴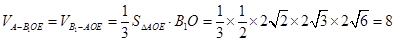 (14分)
(14分)
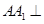 平面ABC,∠
平面ABC,∠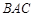 =90°,
=90°,方法1:空间向量法 如图建立空间直角坐标系
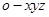 ,
,
因为
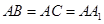 =4,
=4,则
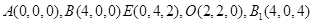
(I)
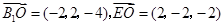 ,
,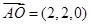
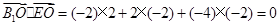 ,∴
,∴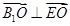 ,∴
,∴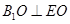
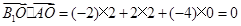 , ∴
, ∴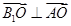 ,∴
,∴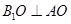
∵

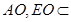 平面
平面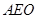 ∴
∴ 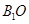 ⊥平面
⊥平面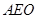 (5分)
(5分)(II) 平面AEO的法向量为
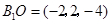 ,设平面 B1AE的法向量为
,设平面 B1AE的法向量为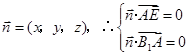 , 即
, 即
令x=2,则
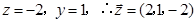
∴
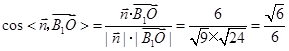
∴二面角B1—AE—F的余弦值为
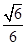 (10分)
(10分)(Ⅲ)因为
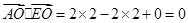 ,∴
,∴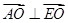 , ∴
, ∴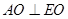
∵
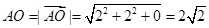 ,
,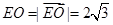
∴
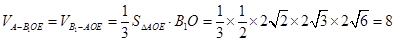 (14 分)
(14 分)方法2:
依题意可知,
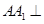 平面ABC,∠
平面ABC,∠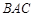 =90°,
=90°,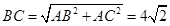 ,∴
,∴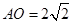
(I)∵
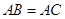 ,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO,
,O为底面圆心,∴BC⊥AO,又∵B1B⊥平面ABC,可证B1O⊥AO, 因为
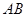 =
=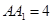 ,则
,则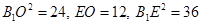 ,∴
,∴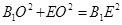
∴B1O⊥EO,∴
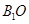 ⊥平面
⊥平面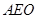 ; (5分)
; (5分)(II)过O做OM⊥AE于点M,连接B1M,
∵B1O⊥平面AEO,可证B1M⊥AE,
∴∠B1MO为二面角B1—AE—O的平面角,
C1C⊥平面ABC,AO⊥OC,可证EO⊥AO,
在Rt△AEO中,可求
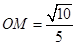 ,
, 在Rt△B1OM中,∠B1OM=90°,∴
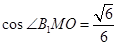
∴二面角B1—AE—O的余弦值为
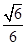 (10分)
(10分)(Ⅲ)因为AB=AC,O为BC的中点,所以
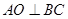
又平面
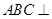 平面
平面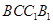 ,且平面
,且平面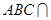 平面
平面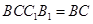 ,
,所以
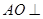 平面
平面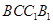 , 故
, 故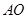 是三棱锥
是三棱锥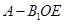 的高
的高∴
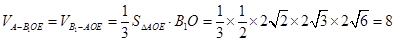 (14分)
(14分)
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
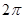 的半圆面,则该圆锥的体积为 .
的半圆面,则该圆锥的体积为 .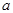 ,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )
,由它的互不相邻的四个顶点连线所构成的四面体的体积是( )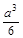



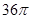 , 则此正方体的表面积是
, 则此正方体的表面积是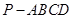 的底面是边长为1的正方形,
的底面是边长为1的正方形,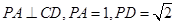
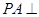 平面
平面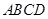
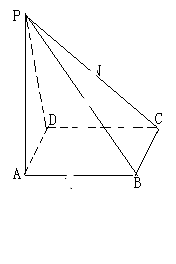




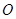 到过球面上A、B、C三点的截面的距离等于此球半径的一半,若
到过球面上A、B、C三点的截面的距离等于此球半径的一半,若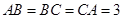 ,则球的体积为 .
,则球的体积为 . 


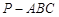 ,
,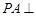 平面
平面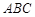 ,
,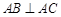 ,
,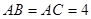 ,
,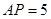 .
.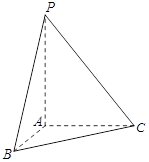
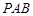 (及其内部)绕
(及其内部)绕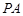 所在直线旋转一周形成一几何体,求该几何体的体积
所在直线旋转一周形成一几何体,求该几何体的体积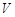 ;
; 的余弦值.
的余弦值.