题目内容
在△ABC中,已知tanB=
,cosA=
,AB边的中线长CD=2,则△ABC的面积为
| 1 |
| 2 |
4
| ||
| 17 |
6
6
.分析:由cosA的值,及A为三角形的内角,利用同角三角函数间的基本关系求出sinA的值,进而确定出tanA的值,再由tanB的值,利用诱导公式及两角和与差的正切函数公式求出tanC的值小于0,可得出C为钝角,根据题意画出相应的图形,过C作CE垂直于AB,在直角三角形AEC与直角三角形BEC中,根据tanA与tanB的值,利用锐角三角函数定义,设EC=x,则有AE=4x,BE=2x,表示出AB,由D为中点,表示出BD,由BD-BE表示出DE,在直角三角形ECD中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,确定出AB与CE的长,利用三角形的面积公式即可求出三角形ABC的面积.
解答: 解:∵cosA=
解:∵cosA=
,A为三角形的内角,
∴sinA=
=
,
∴tanA=
,又tanB=
,
∴tanC=-tan(A+B)=-
=-
<0,
∴C为钝角,
根据题意画出相应的图形,如图所示,
过C作CE⊥AB,交AB于点E,
在Rt△AEC和Rt△BEC中,设EC=x,则有AE=4x,BE=2x,
∴AB=AE+EB=6x,又D为AB的中点,
∴BD=AD=3x,
∴ED=BD-BE=x,
在Rt△EDC中,EC=DE=x,CD=2,
根据勾股定理得:x2+x2=4,
解得:x=
,
则S△ABC=
×6
×
=6.
故答案为:6
 解:∵cosA=
解:∵cosA=4
| ||
| 17 |
∴sinA=
| 1-cos2A |
| ||
| 17 |
∴tanA=
| 1 |
| 4 |
| 1 |
| 2 |
∴tanC=-tan(A+B)=-
| tanA+tanB |
| 1-tanAtanB |
| 6 |
| 7 |
∴C为钝角,
根据题意画出相应的图形,如图所示,
过C作CE⊥AB,交AB于点E,
在Rt△AEC和Rt△BEC中,设EC=x,则有AE=4x,BE=2x,
∴AB=AE+EB=6x,又D为AB的中点,
∴BD=AD=3x,
∴ED=BD-BE=x,
在Rt△EDC中,EC=DE=x,CD=2,
根据勾股定理得:x2+x2=4,
解得:x=
| 2 |
则S△ABC=
| 1 |
| 2 |
| 2 |
| 2 |
故答案为:6
点评:此题属于解三角形的题型,涉及的知识有:同角三角函数间的基本关系,两角和与差的正切函数公式,锐角三角函数定义,以及勾股定理,利用了方程的思想,根据题意画出相应的图形是解本题的关键.

练习册系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.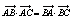 .
. |=|
|=| |;
|; ,求|
,求| -t
-t