题目内容
如图，A、B是单位圆O上的点，C是圆O与x轴正半轴的交点，点A的坐标为
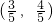，三角形AOB为直角三角形．
（1）求sin∠COA，cos∠COA的值；
（2）求cos∠COB的值．
解：（1）∵A点的坐标为，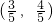
根据三角函数定义可知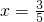
，
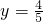，r=1；
∴
，
．
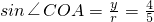（2）∵三角形AOB为直角三角形，
∴∠AOB=90°，
又由（1）知sin∠COA=
，cos∠COA=
；
∴cos∠COB=cos（∠COA+90°）=-sin∠COA=-．
分析：（1）利用任意角的三角函数的定义，先找出x，y，r，代入公式计算．
（2）利用∠AOB=90°，cos∠COB=cos（∠COA+90°）=-sin∠COA=-．
点评：本题考查任意角的三角函数的定义，诱导公式cos（
+θ）=-sinθ 的应用．
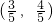，根据三角函数定义可知
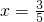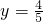，，r=1；∴
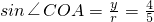，．（2）∵三角形AOB为直角三角形，
∴∠AOB=90°，
又由（1）知sin∠COA=
，cos∠COA=；∴cos∠COB=cos（∠COA+90°）=-sin∠COA=-
．分析：（1）利用任意角的三角函数的定义，先找出x，y，r，代入公式计算．
（2）利用∠AOB=90°，cos∠COB=cos（∠COA+90°）=-sin∠COA=-
．点评：本题考查任意角的三角函数的定义，诱导公式cos（
+θ）=-sinθ 的应用． 
练习册系列答案
相关题目
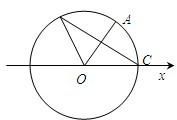如图，A、B是单位圆O上的动点，C是圆与x轴正半轴的交点，设∠COA=α．
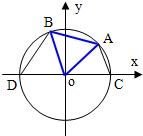如图，A、B是单位圆O上的点，C、D分别是圆O与x轴的两个交点，△ABO为正三角形．
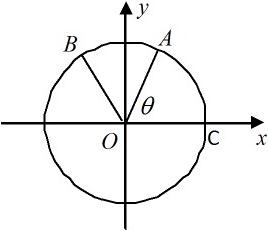如图：A、B是单位圆上的动点，C是单位圆与x轴正半轴的交点，
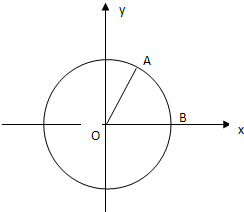如图，A，B是单位圆上的两个质点，B点坐标为（1，0），∠BOA=60°，质点A以1弧度/秒的角速度按逆时针方向在单位圆上运动；质点B以1弧度/秒的角速度按顺时针方向在单位圆上运动，过点A作AA1⊥y轴于A1，过点B作BB1⊥y轴于B1．
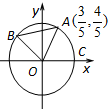如图，A、B是单位圆O上的点，C是圆O与x轴正半轴的交点，点A的坐标为