题目内容
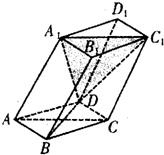 如图,棱柱ABCD-A1B1C1D1的底面和侧棱长都等于2,平面A1ACC1 AA1C1C⊥ABCD,∠A1AC=60°.点O为底面对角线AC与BD的交点.
如图,棱柱ABCD-A1B1C1D1的底面和侧棱长都等于2,平面A1ACC1 AA1C1C⊥ABCD,∠A1AC=60°.点O为底面对角线AC与BD的交点.(1)证明:A1O⊥平面ABCD;
(2)求二面角D-A1A-C的平面角的正切值.
分析:(1)证明△ABC为等边三角形,由余弦定理可得 A1O2=3,由勾股定理可得A1O⊥AO,再由面AA1C1C⊥平面ABCD,得到 A1O⊥平面ABCD.
(2)过点O 作OE⊥AA1,∠DEO即为二面角D-A1A-C的平面角勾股定理求的OD,Rt△AEO中,利用边角关系求得 EO,由tan∠DEO=
求得结果.
(2)过点O 作OE⊥AA1,∠DEO即为二面角D-A1A-C的平面角勾股定理求的OD,Rt△AEO中,利用边角关系求得 EO,由tan∠DEO=
| OD |
| OE |
解答:解:(1)证明:由已知得 AB=BC=2,∠ABC=60°,∴△ABC为等边三角形,∴AC=2.
又O为AC的中点,故 OA=1,△A1OA中,由余弦定理可得 A1O2=3,∴A1O2+AO2=A1A2,
∴A1O⊥AO.又因平面AA1C1C⊥平面ABCD,∴A1O⊥平面ABCD.
(2)因底面ABCD为菱形,则 BD⊥AC,又 BD⊥A1O,则BD⊥面C1C.过点O 作OE⊥AA1 ,
则AA1⊥DE,∠DEO即为二面角D-A1A-C的平面角.OD=
=
,
Rt△AEO中,EO=AO•sin∠EAO=
.
在Rt△DEO中,tan∠DEO=
=2,故二面角D-A1A-C的平面角的正切值等于 2.
又O为AC的中点,故 OA=1,△A1OA中,由余弦定理可得 A1O2=3,∴A1O2+AO2=A1A2,
∴A1O⊥AO.又因平面AA1C1C⊥平面ABCD,∴A1O⊥平面ABCD.
(2)因底面ABCD为菱形,则 BD⊥AC,又 BD⊥A1O,则BD⊥面C1C.过点O 作OE⊥AA1 ,
则AA1⊥DE,∠DEO即为二面角D-A1A-C的平面角.OD=
| AB2 -AO2 |
| 3 |
Rt△AEO中,EO=AO•sin∠EAO=
| ||
| 2 |
在Rt△DEO中,tan∠DEO=
| OD |
| OE |
点评:本题考查证明线线垂直、线面垂直的方法,求二面角的平面角的正切值,找出二面角的平面角是解题的难点.

练习册系列答案
相关题目
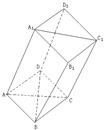 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC和∠A1B1C1均为60°,平面AA1C1C⊥平面ABCD. 如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.
如图四棱柱ABCD-A1B1C1D1的底面ABCD为正方形,侧棱与底边长均为a,且∠A1AD=∠A1AB=60°.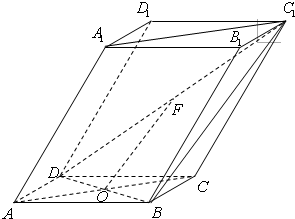 17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.
17、如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,AC∩BD=O,侧棱AA1⊥BD,点F为DC1的中点.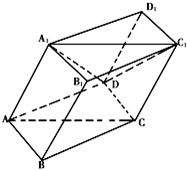 如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?
如图,棱柱ABCD-A1B1C1D1的底面ABCD为菱形,平面AA1C1C⊥平面ABCD.?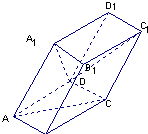 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1CC1⊥平面ABCD,∠A1AC=60°