题目内容
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求圆![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() ,直线
,直线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数),已知
为参数),已知![]() 与圆
与圆![]() 交于
交于![]() 两点,且
两点,且![]() ,求
,求![]() 的普通方程.
的普通方程.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】分析:(1)利用![]() 代入
代入![]() ,即可得圆
,即可得圆![]() 的直角坐标方程;(2)将直线
的直角坐标方程;(2)将直线![]() 的参数方程
的参数方程![]() 代入圆
代入圆![]() 的直角坐标方程
的直角坐标方程![]() 中,化简得
中,化简得![]() ,利用韦达定理以及直线参数的几何意义可得
,利用韦达定理以及直线参数的几何意义可得![]() ,从而可得结果.
,从而可得结果.
详解:(1)将![]()
代入圆![]() 的极坐标方程
的极坐标方程![]() ,
,
得![]() ,
,
化为圆的标准方程为![]() .
.
(2)将直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)
为参数)
代入圆![]() 的直角坐标方程
的直角坐标方程![]() 中,化简得
中,化简得![]() ,
,
设![]() 两点所对应的参数分别为
两点所对应的参数分别为![]() ,
,
由韦达定理知![]() ①
①
∴![]() 同号 又∵
同号 又∵![]() , ∴
, ∴![]() ②
②
由①②可知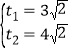 或
或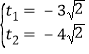
∴![]() 或
或![]() 解得
解得![]() ,∴
,∴![]() ,
,
∴![]() 的普通方程为
的普通方程为![]() .
.

练习册系列答案
相关题目
【题目】为了引导居民合理用水,某市决定全面实施阶梯水价.阶梯水价原则上以住宅(一套住宅为一户)的月用水量为基准定价,具体划分标准如表:
阶梯级别 | 第一阶梯水量 | 第二阶梯水量 | 第三阶梯水量 |
月用水量范围(单位:立方米) |
|
|
|
从本市随机抽取了10户家庭,统计了同一月份的月用水量,得到如图茎叶图:

(1)现要在这10户家庭中任意选取3家,求取到第二阶梯水量的户数![]() 的分布列与数学期望;
的分布列与数学期望;
(2)用抽到的10户家庭作为样本估计全市的居民用水情况,从全市依次随机抽取10户,若抽到![]() 户月用水量为二阶的可能性最大,求
户月用水量为二阶的可能性最大,求![]() 的值.
的值.