题目内容
已知a<1,解关于x的不等式
>1.
| ax | x-2 |
分析:
>1⇒
>0,利用a-1<0,可得
<0,通过对a的范围的讨论,即可求得相应情况下的解集.
| ax |
| x-2 |
| (a-1)x+2 |
| x-2 |
x-
| ||
| x-2 |
解答:解:不等式
>1可化为
>0.
∵a<1,
∴a-1<0,则原不等式可化为
<0,___________(5分
当0<a<1时,0<1-a<1,
>2,∴原不等式的解集为{x|2<x<
};
当a=0时,原不等式的解集为∅;
当a<0时,同理可求原不等式的解集为{x|
<x<2}.___________(10分)
| ax |
| x-2 |
| (a-1)x+2 |
| x-2 |
∵a<1,
∴a-1<0,则原不等式可化为
x-
| ||
| x-2 |
当0<a<1时,0<1-a<1,
| 2 |
| 1-a |
| 2 |
| 1-a |
当a=0时,原不等式的解集为∅;
当a<0时,同理可求原不等式的解集为{x|
| 2 |
| 1-a |
点评:本题考查分式不等式的解法,着重考查分类讨论思想的应用,对参数a分类讨论时,比较两根的大小是难点,属于中档题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
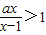 .
.