题目内容
已知a<1,解关于x的不等式| ax | x-1 |
分析:这是一个含有字母系数的不等式,仔细观察原不等式,通过去分母、移项并合并得到:
>0,再对于字母a分情况讨论,即可求得解集.
| (a-1)x+1 |
| x-1 |
解答:解:原不等式可化为
-1>0?
>0?
>0
?((a-1)x+1)(x-1)>0?(x+
)(x-1)<0(∵a<1,
∴a-1<0)------------------(4分)
10当-
=1,即a=0时,原不等式等价于(x-1)2<0⇒x∈?;----(6分)
20当-
>1,即a>0时,原不等式等价于1<x<
;---------------(8分)
30当-
<1,即a<0时,原不等式等价于
<x<1.---------------(10分)
综上所述:
当a<0时,原不等式的解集为(
,1);---------------------------------------(11分)
当a=0时,原不等式的解集为?;--------------------------------------------------(12分)
当a>0时,原不等式的解集为(1,
).----------------------------------------(13分)
| ax |
| x-1 |
| ax-x+1 |
| x-1 |
| (a-1)x+1 |
| x-1 |
?((a-1)x+1)(x-1)>0?(x+
| 1 |
| a-1 |
∴a-1<0)------------------(4分)
10当-
| 1 |
| a-1 |
20当-
| 1 |
| a-1 |
| 1 |
| 1-a |
30当-
| 1 |
| a-1 |
| 1 |
| 1-a |
综上所述:
当a<0时,原不等式的解集为(
| 1 |
| 1-a |
当a=0时,原不等式的解集为?;--------------------------------------------------(12分)
当a>0时,原不等式的解集为(1,
| 1 |
| 1-a |
点评:本题考查了不等式的性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.注意分四种情况讨论.
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.注意分四种情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
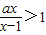 .
.