题目内容
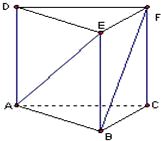 如图,三棱柱ABC-DEF的侧面为全等的矩形,且底面边长为
如图,三棱柱ABC-DEF的侧面为全等的矩形,且底面边长为 .
.
(1)若侧棱长为2,求直线AE与BF所成的角;
(2)若直线AE⊥BF,求侧棱的长.
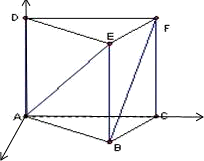 解:建立如图所示坐标系
解:建立如图所示坐标系(1)根据题意有:A(0,0,0),E(
 ,
, ,2),B(
,2),B( ,
, ,0),F(0,
,0),F(0, ,2)
,2)∴
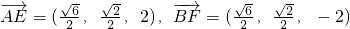
∴cos<
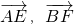 >=0
>=0∴直线AE与BF所成的角为90°.
(2)设侧棱长为:x(x>0)
则有:A(0,0,0),E(
 ,
, ,x),B(
,x),B( ,
, ,0),F(0,
,0),F(0, ,x)
,x)∴
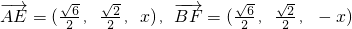
∵直线AE⊥BF
∴
 =0
=0∴x2=4
∴x=2
故侧棱的长为2
分析:(1)先求得相关点:A(0,0,0),E(
 ,
, ,2),B(
,2),B( ,
, ,0),F(0,
,0),F(0, ,2)的坐标,进而求得相关向量
,2)的坐标,进而求得相关向量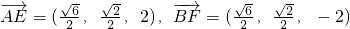 的坐标,再用向量的夹角公式求解.
的坐标,再用向量的夹角公式求解.(2)按照(1)的思路相关点的竖坐标用x表示,从而向量的竖坐标也用x表示,因为两直线垂直,所以相应向量的数量积为零,从而求得x的值.
点评:本题主要考查空间几体的结构特征及向量法研究空间角和线线垂直的问题,同时还考查了转化思想和运算能力,属中档题.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目

 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC.
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,AB⊥AC,D、E分别为AA1、B1C的中点,AB=AC. (2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC=
(2012•黑龙江)如图,三棱柱ABC-A1B1C1中,侧棱垂直底面,∠ACB=90°,AC=BC= 如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB
如图,三棱柱ABC-A1B1C1的底面ABC为正三角形,侧棱AA1⊥平面ABC,D是BC中点,且AA1=AB (2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=
(2012•大连二模)如图,三棱柱ABC-A′B′C′,cc′=