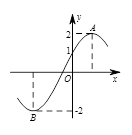题目内容
已知函数 (其中
(其中 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为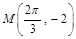 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)当 ,求
,求 的值域.
的值域.
 (其中
(其中 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为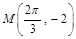 .
.(Ⅰ)求
 的解析式;
的解析式;(Ⅱ)当
 ,求
,求 的值域.
的值域.(Ⅰ)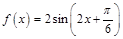 ;(Ⅱ)
;(Ⅱ) 值域为
值域为 .
.
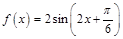 ;(Ⅱ)
;(Ⅱ) 值域为
值域为 .
.试题分析:(Ⅰ)首先由函数图象上一个最低点为
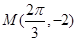 ,得A=2.又函数图象与x轴的交点中,相邻两个交点之间的距离为
,得A=2.又函数图象与x轴的交点中,相邻两个交点之间的距离为 ,所以
,所以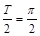 ,由此可求得
,由此可求得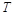 的值,进而可求得
的值,进而可求得 的值.利用函数图象上一个最低点为
的值.利用函数图象上一个最低点为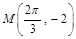 ,由代入法或关键点法可求得
,由代入法或关键点法可求得 的值,最后得函数
的值,最后得函数 的解析式;(Ⅱ)在(Ⅰ)的基础上首先写出
的解析式;(Ⅱ)在(Ⅰ)的基础上首先写出 的表达式,利用三角函数的有关公式,将其化为一个复合角的三角函数,利用整体思想来求函数
的表达式,利用三角函数的有关公式,将其化为一个复合角的三角函数,利用整体思想来求函数 的值域.
的值域.试题解析:(1)由最低点为
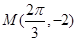 ,得A=2.由x轴上相邻的两个交点之间的距离为
,得A=2.由x轴上相邻的两个交点之间的距离为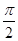 ,得
,得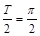 ,即
,即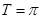 ,
,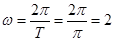 ,由点
,由点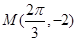 在图像上得
在图像上得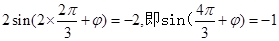
故
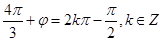 ,
,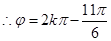 ,又
,又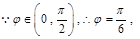

6分
(2)
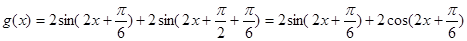 ,
,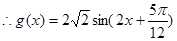 .因为
.因为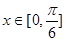 ,则
,则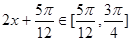 ,所以
,所以 值域为
值域为 .
.12分

练习册系列答案
相关题目
 ,
, .求:
.求: 的最小值及取得最小值的自变量
的最小值及取得最小值的自变量 的集合;
的集合;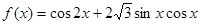
 的值域,并写出函数
的值域,并写出函数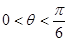 ,且
,且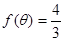 ,计算
,计算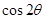 的值.
的值.

 ,函数
,函数 .
. 的单调递增区间;
的单调递增区间; 成立的
成立的 的取值集合.
的取值集合.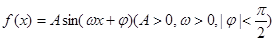 的图象的一部分如下图所示.
的图象的一部分如下图所示.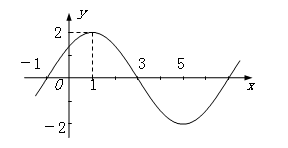
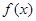 的解析式;
的解析式;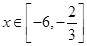 时,求函数
时,求函数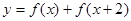 的最大值与最小值及相应的
的最大值与最小值及相应的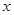 的值.
的值. 在
在 上的图像大致为( )
上的图像大致为( )
 的图象按向量
的图象按向量 =(-
=(- ,0)平移,所得曲线的一部分如图所示,则
,0)平移,所得曲线的一部分如图所示,则 ,
, 的值分别是( )
的值分别是( )
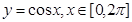 的图象和直线
的图象和直线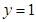 围成一个封闭的平面图形,这个封闭图形的面积是_____________;
围成一个封闭的平面图形,这个封闭图形的面积是_____________;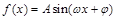 (其中
(其中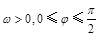 )的部分图象,其中
)的部分图象,其中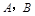 两点之间的距离为
两点之间的距离为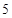 ,那么
,那么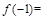 ( )
( )