题目内容
已知双曲线 的离心率为
的离心率为 ,焦距为2c,且2a2=3c,双曲线 上一点P满足
,焦距为2c,且2a2=3c,双曲线 上一点P满足 (F1、F2为左右焦点),则|
(F1、F2为左右焦点),则| |•|
|•| |=________.
|=________.
4
分析:根据双曲线的离心率为 ,得到可得a=
,得到可得a= c,从而b=
c,从而b= c,再根据2a2=3c,联解关于a、c的式子,得到a=
c,再根据2a2=3c,联解关于a、c的式子,得到a= ,b=1,c=2,从而得到双曲线方程为
,b=1,c=2,从而得到双曲线方程为 .接下来根据双曲线的定义,得到
.接下来根据双曲线的定义,得到 -
- =
= ,结合
,结合 ,在三角形PF1F2中利用余弦定理,联解关于
,在三角形PF1F2中利用余弦定理,联解关于 •
• 的等式,可得
的等式,可得 •
• =4.
=4.
解答:∵双曲线 的离心率为
的离心率为 ,
,
∴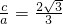 ,可得a=
,可得a= c,从而b=
c,从而b= =
= c
c
又∵2a2=3c,即2( c)2=3c,
c)2=3c,
∴c=2,a= ,b=1,可得双曲线方程为
,b=1,可得双曲线方程为
∵点P在双曲线上,∴根据双曲线的定义,得 -
- =
=
因此( -
- )2=12,即
)2=12,即 2-2
2-2 •
• +
+ 2=12…①
2=12…①
∵
∴cosP= =
=
结合 =2c=4,化简整理得:即
=2c=4,化简整理得:即 2+
2+ 2=20,代入①,可得
2=20,代入①,可得 •
• =4
=4
故答案为:4
点评:本题给出双曲线上一点对两个焦点构成的向量的数量积,要求两个向量模的积,着重考查了向量在几何中的应用与双曲线的定义与简单几何性质等知识点,属于中档题.
分析:根据双曲线的离心率为
 ,得到可得a=
,得到可得a= c,从而b=
c,从而b= c,再根据2a2=3c,联解关于a、c的式子,得到a=
c,再根据2a2=3c,联解关于a、c的式子,得到a= ,b=1,c=2,从而得到双曲线方程为
,b=1,c=2,从而得到双曲线方程为 .接下来根据双曲线的定义,得到
.接下来根据双曲线的定义,得到 -
- =
= ,结合
,结合 ,在三角形PF1F2中利用余弦定理,联解关于
,在三角形PF1F2中利用余弦定理,联解关于 •
• 的等式,可得
的等式,可得 •
• =4.
=4.解答:∵双曲线
 的离心率为
的离心率为 ,
,∴
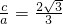 ,可得a=
,可得a= c,从而b=
c,从而b= =
= c
c又∵2a2=3c,即2(
 c)2=3c,
c)2=3c,∴c=2,a=
 ,b=1,可得双曲线方程为
,b=1,可得双曲线方程为
∵点P在双曲线上,∴根据双曲线的定义,得
 -
- =
=
因此(
 -
- )2=12,即
)2=12,即 2-2
2-2 •
• +
+ 2=12…①
2=12…①∵

∴cosP=
 =
=
结合
 =2c=4,化简整理得:即
=2c=4,化简整理得:即 2+
2+ 2=20,代入①,可得
2=20,代入①,可得 •
• =4
=4故答案为:4
点评:本题给出双曲线上一点对两个焦点构成的向量的数量积,要求两个向量模的积,着重考查了向量在几何中的应用与双曲线的定义与简单几何性质等知识点,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 的离心率为2,焦点到渐近线的距离等于
的离心率为2,焦点到渐近线的距离等于 ,过右焦点
,过右焦点 的直线
的直线
 、
、 两点,
两点, 为左焦点,
为左焦点, 的面积等于
的面积等于 ,求直线
,求直线 的方程.
的方程. 的离心率为2,焦点到渐近线的距离为
的离心率为2,焦点到渐近线的距离为 ,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
,点P的坐标为(0,-2),过P的直线l与双曲线C交于不同两点M、N.
 (O为坐标原点),求t的取值范围
(O为坐标原点),求t的取值范围