题目内容
已知⊙O:x2+y2=a2,A(-a,0),B(a,0),P1、P2是⊙O上关于x轴对称的两点,则直线AP1与直线BP2的交点P的轨迹方程为
- A.x2+y2=2a2
- B.x2+y2=4a2
- C.x2-y2=4a2
- D.x2-y2=a2
D
分析:求出直线AP1与直线BP2的方程,将两方程联立解出其交点P的坐标满足的方程即可.
解答:设P1(x0,y0),则P2(x0,-y0),则直线AP1的方程为:y=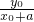 (x+a) ①
(x+a) ①
直线BP2的方程为:y= (x-a) ②
(x-a) ②
①×②得
y2= (x2-a2) ③
(x2-a2) ③
又∵P1(x0,y0)在圆上,
∴x02+y02=a2即a2-x02=y02
所以③式可化为:y2=(x2-a2)=x2-a2
即x2-y2=a2,这就是P点的轨迹方程.
故应选D.
点评:本题考查求两直线交点的轨迹方程,在设出两个直线的方程联立求交点满足的方程时,用两式相乘的方法构造出可以整体消元得到点P的坐标满足方程的形式,消元的技巧较强,答题者应细心体会.
分析:求出直线AP1与直线BP2的方程,将两方程联立解出其交点P的坐标满足的方程即可.
解答:设P1(x0,y0),则P2(x0,-y0),则直线AP1的方程为:y=
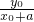 (x+a) ①
(x+a) ①直线BP2的方程为:y=
 (x-a) ②
(x-a) ②①×②得
y2=
 (x2-a2) ③
(x2-a2) ③又∵P1(x0,y0)在圆上,
∴x02+y02=a2即a2-x02=y02
所以③式可化为:y2=(x2-a2)=x2-a2
即x2-y2=a2,这就是P点的轨迹方程.
故应选D.
点评:本题考查求两直线交点的轨迹方程,在设出两个直线的方程联立求交点满足的方程时,用两式相乘的方法构造出可以整体消元得到点P的坐标满足方程的形式,消元的技巧较强,答题者应细心体会.

练习册系列答案
相关题目
 已知⊙O:x2+y2=1和点M(4,2).
已知⊙O:x2+y2=1和点M(4,2). 如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.
如图,已知点A(-2,0),点P是⊙B:(x-2)2+y2=36上任意一点,线段AP的垂直平分线交BP于点Q,点Q的轨迹记为曲线C.