题目内容
【题目】设![]() .
.
(1)若![]() ,且
,且![]() 为函数
为函数![]() 的一个极值点,求函数
的一个极值点,求函数![]() 的单调递增区间;
的单调递增区间;
(2)若![]() ,且函数
,且函数![]() 的图象恒在
的图象恒在![]() 轴下方,其中
轴下方,其中![]() 是自然对数的底数,求实数
是自然对数的底数,求实数![]() 的取值范围.
的取值范围.
【答案】(1)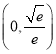 ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)求出![]() 的导函数,由
的导函数,由![]() 为函数
为函数![]() 的一个极值点,则
的一个极值点,则![]() ,即可求出参数
,即可求出参数![]() 的值,解
的值,解![]() 得到函数的单调递增区间.
得到函数的单调递增区间.
(2)依题意,![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,利用导数研究函数的单调性、极值,则
,利用导数研究函数的单调性、极值,则![]() 的极小值需大于零,再次构造函数求出参数的取值范围.
的极小值需大于零,再次构造函数求出参数的取值范围.
解:(1)![]() ,
,![]() ,由题意
,由题意![]() ,所以
,所以![]() ,所以
,所以![]() ,令
,令![]() ,得
,得![]() 或
或![]() ,当
,当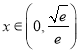 时,
时,![]() ,当
,当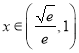 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以函数
,所以函数![]() 的单调递增区间是
的单调递增区间是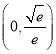 和
和![]() ;
;
(2)依题意,![]() ,即
,即![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,则
,则![]() .
.
对于![]() ,
,![]() ,故其必有两个零点,且两个零点的积为-1,
,故其必有两个零点,且两个零点的积为-1,
则两个零点一正一负,设其中一个零点为![]() ,
,
则![]() ,即
,即![]() ,
,
且![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() ,即
,即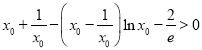 ,
,
令![]() ,
,
则![]()
![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,则
,则![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又
上单调递减,又![]() ,故
,故![]() ,显然函数
,显然函数![]() 在
在![]() 上是关于
上是关于![]() 的单调递增函数,则
的单调递增函数,则![]() ,故实数
,故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目