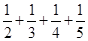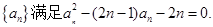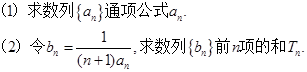题目内容
设数列 的前
的前 项和为
项和为 ,且满足
,且满足
 .
.
(1)求 ,
, ,
, ,
, 的值并写出其通项公式;(2)证明数列
的值并写出其通项公式;(2)证明数列 是等比数列.
是等比数列.
 的前
的前 项和为
项和为 ,且满足
,且满足
 .
.(1)求
 ,
, ,
, ,
, 的值并写出其通项公式;(2)证明数列
的值并写出其通项公式;(2)证明数列 是等比数列.
是等比数列.(Ⅰ)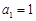 ;
;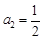 ;
;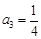 ;
;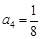 。
。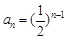 ;(2)详见解析
;(2)详见解析
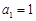 ;
;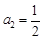 ;
;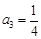 ;
;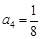 。
。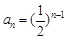 ;(2)详见解析
;(2)详见解析试题分析:(1)由
 ,得
,得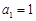 ;
;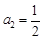 ;
;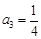 ;
;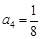 ,故可猜想
,故可猜想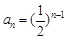 。(2)根据已知
。(2)根据已知 和
和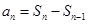 可推导出
可推导出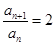 。根据等比数列的定义可知,数列
。根据等比数列的定义可知,数列 是首项为1公比为2的等比数列。
是首项为1公比为2的等比数列。解:(1)由
 ,得
,得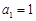 ;
;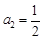 ;
;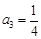 ;
;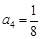 ,
,猜想
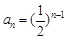
 . 6分
. 6分(2)方法一:
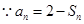 ①
① 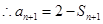 ②
②②-①得
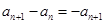 ∴
∴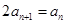 即
即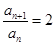
∴数列
 是等比数列. 13分
是等比数列. 13分方法二:(三段论)∵通项公式为
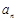 的数列
的数列 ,若
,若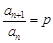 ,
,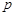 是非零常数,则
是非零常数,则 是等比数列;
是等比数列;由(1)通项公式
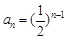 ,即
,即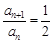 ;∴通项公式
;∴通项公式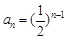 的数列
的数列 是等比数列.
是等比数列.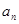 与
与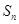 的关系;2等比数列的定义。
的关系;2等比数列的定义。
练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 ,数列
,数列 的前
的前 项和为
项和为 ,点
,点 均在函数
均在函数 的图象上.
的图象上. ;
;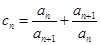 ,证明:
,证明: .
.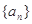 的前n项和记为
的前n项和记为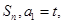 点
点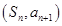 在直线
在直线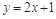 上,
上,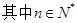 .(1)若数列
.(1)若数列 是等比数列,求实数
是等比数列,求实数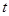 的值;
的值;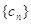 中,所有满足
中,所有满足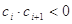 的整数
的整数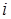 的个数称为这个数列
的个数称为这个数列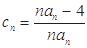 (
(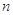
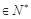 ),在(1)的条件下,求数列
),在(1)的条件下,求数列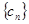 中,所有满足
中,所有满足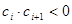 的正整数
的正整数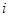 的个数称为这个数列
的个数称为这个数列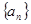 的前
的前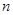 项和
项和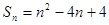 ,
,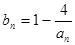 (
(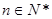 ),则数列
),则数列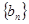 的变号数为 .
的变号数为 . 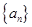 满足
满足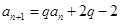 (
(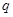 为常数,
为常数,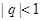 ),若
),若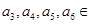
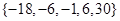 ,则
,则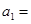 .
. ,当
,当 时,
时, ( )
( )