题目内容
已知向量 .
.
(1)当a∥b时,求2cos2x-sin2x的值;
(2)求f(x)=(a+b)•b在 上的单调区间,并说明单调性.
上的单调区间,并说明单调性.
解:(1)因为 ,所以
,所以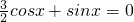 ,所以tanx=
,所以tanx= ,
,
所以2cos2x-sin2x= =
= =
= .
.
(2)由题意可得:f(x)= ,
,
∵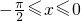 ,
,
∴ ,令
,令 ,得
,得 ,
,
故f(x) 在 上是单调减函数,
上是单调减函数,
同理f(x) 在 上是单调增函数.
上是单调增函数.
分析:(1)由题意可得: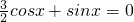 ,所以tanx=
,所以tanx= ,所以2cos2x-sin2x=
,所以2cos2x-sin2x= =
= ,进而得到答案.
,进而得到答案.
(2)由题意可得:f(x)= ,并且
,并且 ,令
,令 ,进而得到函数的减区间,同理可得增区间.
,进而得到函数的减区间,同理可得增区间.
点评:解决此类问题的关键是熟练掌握向量的数量积的运算,以及三角函数的有关性质.
 ,所以
,所以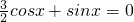 ,所以tanx=
,所以tanx= ,
,所以2cos2x-sin2x=
 =
= =
= .
.(2)由题意可得:f(x)=
 ,
,∵
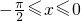 ,
,∴
 ,令
,令 ,得
,得 ,
,故f(x) 在
 上是单调减函数,
上是单调减函数,同理f(x) 在
 上是单调增函数.
上是单调增函数.分析:(1)由题意可得:
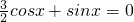 ,所以tanx=
,所以tanx= ,所以2cos2x-sin2x=
,所以2cos2x-sin2x= =
= ,进而得到答案.
,进而得到答案.(2)由题意可得:f(x)=
 ,并且
,并且 ,令
,令 ,进而得到函数的减区间,同理可得增区间.
,进而得到函数的减区间,同理可得增区间.点评:解决此类问题的关键是熟练掌握向量的数量积的运算,以及三角函数的有关性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目