题目内容
设角α、β是锐角,则“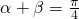 ”是“(1+tanα)(1+tanβ)=2”成立的
”是“(1+tanα)(1+tanβ)=2”成立的
- A.充分非必要条件
- B.必要非充分条件
- C.充要条件
- D.既非充分也非必要条件
C
分析:先根据α,β均为锐角且α+β= 求出tanα、tanβ的关系式,再将(1+tanα)(1+tanβ)展开h化简,判断即可.
求出tanα、tanβ的关系式,再将(1+tanα)(1+tanβ)展开h化简,判断即可.
解答:∵α,β均为锐角,α+β= ,
,
?tan(α+β)= =1,
=1,
?tanα+tanβ=1-tanαtanβ,?tanα+tanβ+tanαtanβ=1
?(1+tanα)(1+tanβ)=1+tanα+tanβ+tanαtanβ=1+1=2
所以角α、β是锐角,则“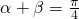 ”是“(1+tanα)(1+tanβ)=2”成立的充要条件.
”是“(1+tanα)(1+tanβ)=2”成立的充要条件.
故选C.
点评:本题主要考查两角和的正切公式.充要条件的判断方法,属基础题.
分析:先根据α,β均为锐角且α+β=
 求出tanα、tanβ的关系式,再将(1+tanα)(1+tanβ)展开h化简,判断即可.
求出tanα、tanβ的关系式,再将(1+tanα)(1+tanβ)展开h化简,判断即可.解答:∵α,β均为锐角,α+β=
 ,
,?tan(α+β)=
 =1,
=1,?tanα+tanβ=1-tanαtanβ,?tanα+tanβ+tanαtanβ=1
?(1+tanα)(1+tanβ)=1+tanα+tanβ+tanαtanβ=1+1=2
所以角α、β是锐角,则“
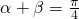 ”是“(1+tanα)(1+tanβ)=2”成立的充要条件.
”是“(1+tanα)(1+tanβ)=2”成立的充要条件.故选C.
点评:本题主要考查两角和的正切公式.充要条件的判断方法,属基础题.

练习册系列答案
 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 是锐角,则“
是锐角,则“ ”是“
”是“ ”成立的 ( )
”成立的 ( )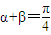 ”是“(1+tanα)(1+tanβ)=2”成立的( )
”是“(1+tanα)(1+tanβ)=2”成立的( )