题目内容
如图,Rt△ABC在平面α内,点P在平面α外,P到直角顶点A的距离为8,到两条直角边的距离均为![]() ,求:
,求:

(1)P到平面α的距离;
(2)PA与平面α所成角的正弦值.
答案:
解析:
解析:
|
[解析](1)如题图,过P作PO⊥α于点O,作OD⊥AB于点D,连结PD. 则PO⊥AB,于是AB⊥平面POD,从而AD⊥PD,故PD= 同理,作OE⊥AC于E点,则AE= ∴矩形ADOE为正方形. ∴ ∴ (2)由(1)可知,∠PAO便是所求PA与平面α所成的角. sin∠PAO= [分析](1)要求P到平面α的距离,于是我们过P作PO⊥α于点O,利用勾股定理得到AD和AE的长相等,从而知ADOE为正方形,易求得AO的长,从而在Rt△PAO中利用勾股定理得到PO的长度即为P到平面α的距离. (2)容易证明∠PAO即为PA与平面α所成角,可在Rt△PAO中应用勾股定理求得. |

练习册系列答案
相关题目
如图,Rt△ABC中,AC⊥BC,D在边AC上,已知BC=2,CD=1,∠ABD=45°,则AD=( )


| A、2 | B、5 | C、4 | D、1 |
 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-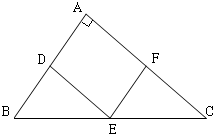 如图,Rt△ABC内有一内接正方形ADEF,它的两条边AD,AF分别在直角边AB,AC上.设BC=a,∠ABC=θ.
如图,Rt△ABC内有一内接正方形ADEF,它的两条边AD,AF分别在直角边AB,AC上.设BC=a,∠ABC=θ. 如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,-
如图,Rt△ABC的顶点坐标A(-3,0),直角顶点B(-1,- ),顶点C在x轴上.
),顶点C在x轴上.