题目内容
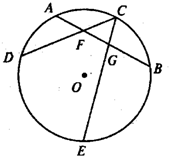 如图.过⊙O的弧AB的中点C作弦CD,CE分别与AB相交于点F,G.
如图.过⊙O的弧AB的中点C作弦CD,CE分别与AB相交于点F,G.
求证:CD•CF=CE•CG.
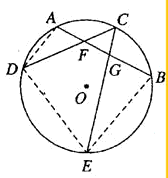 证明:连接AD,DE,EB,
证明:连接AD,DE,EB,由A,D,E,B四点共圆,得∠ADE+∠B=180°
∵∠ADE=∠ADC+∠CDE
∴∠ADC+∠CDE+∠B=180°①
∵点C是弧AB的中点,
∴∠ADC=∠BEC ②
由①②,得∴∠BEC+∠CDE+∠B=180°,即(∠BEC+∠B)+∠CDE=180°,∴∠EGA+∠CDE=180°,则四边形DFEG内接于圆
∵直线CFD,CGE是该圆的两条割线
∴CD×CF=CG×CE
分析:分析知,若能证明四点DFGE共圆,则可以有割线定理证得CD•CF=CE•CG,由北证明目标确定,在图形中连接DE,证明四点共圆即可.
点评:本题考查与圆有关的比例线段,解本题的关键是由所证的结论观察出其成立的等价条件四点DFGE共圆,在几何证明中确定好解决问题的方向对顺利解题很关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
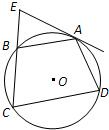 附加题:
附加题: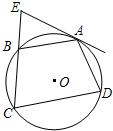 A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点.
A.如图,四边形ABCD内接于⊙O,弧AB=弧AD,过A点的切线交CB的延长线于E点. 22、如图.过⊙O的弧AB的中点C作弦CD,CE分别与AB相交于点F,G.
22、如图.过⊙O的弧AB的中点C作弦CD,CE分别与AB相交于点F,G. =M
=M ,试求二阶矩阵M.
,试求二阶矩阵M. ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和. .
.