题目内容
下列四个函数中,满足f(x+1)=2f(x),(x∈R)的只能是( )
分析:分别将函数一一代入,通过计算可以验证,从而可得结论
解答:解:对于A,f(x+1)=
,2f(x)=x,∴f(x+1)≠2f(x)
对于B,f(x+1)=x+
,2f(x)=2x+1,∴f(x+1)≠2f(x)
对于C,f(x+1)=2x+1,2f(x)=2×2x=2x+1,∴f(x+1)=2f(x)
对于D,f(x+1)=log
(x+1),2f(x)=2log
x,∴f(x+1)≠2f(x)
故选C.
| x+1 |
| 2 |
对于B,f(x+1)=x+
| 3 |
| 2 |
对于C,f(x+1)=2x+1,2f(x)=2×2x=2x+1,∴f(x+1)=2f(x)
对于D,f(x+1)=log
| 1 |
| 2 |
| 1 |
| 2 |
故选C.
点评:本题以函数的递推关系为载体,考查函数解析式的求解,解题的关键是一一代入,并且正确计算

练习册系列答案
相关题目
在下列四个函数中,满足性质:“对于区间(1,2)上的任意x1,x2(x1≠x2),|f(x1)-f(x2)|<|x2-x1|恒成立”的只有( )
A、f(x)=
| ||
| B、f(x)=|x| | ||
| C、f(x)=2x | ||
| D、f(x)=x2 |
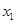 ,
, (
( ).
). 恒成立”的只有
恒成立”的只有  B.
B.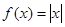 C.
C. D.
D.
 上任意
上任意 ,
,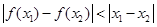 恒成立”的只有 (
)
恒成立”的只有 (
) B.
B.
 D.
D.