题目内容
△ABC的三边a,b,c的倒数成等差数列,则b边所对的角为
- A.锐角
- B.钝角
- C.直角
- D.不能确定
A
分析:方法一:使用余弦定理,由已知求出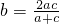 ,计算cosB=
,计算cosB= 的符号,进而可求B的范围
的符号,进而可求B的范围
方法二:反证法,假设 ,则 b为最大边,有b>a>0,b>c>0,结合已知进行推导可求
,则 b为最大边,有b>a>0,b>c>0,结合已知进行推导可求
方法三:反证法由题意可得 =
= ,故b边不是最大边,也不是最小边.假设B≥
,故b边不是最大边,也不是最小边.假设B≥ ,则最大边所对的角大于
,则最大边所对的角大于  ,这与三角形内角和相矛盾,从而可得
,这与三角形内角和相矛盾,从而可得
解答:方法一:由题意可得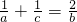 .
.
∴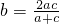 ,
,
∵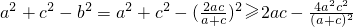 =
=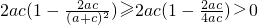 .
.
即cosB= >0
>0
故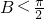
法2:反证法:假设
则有b>a>0,b>c>0.
则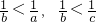
可得 与已知矛盾,
与已知矛盾,
假设不成立,原命题正确.
(法三)∵△ABC的三边a,b,c的倒数成等差数列,
∴ =
= ,故b边不是最大边,也不是最小边.
,故b边不是最大边,也不是最小边.
若B≥ ,则最大边所对的角大于
,则最大边所对的角大于  ,这与三角形内角和相矛盾,故
,这与三角形内角和相矛盾,故 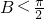 .
.
点评:本题主要考查了利用余弦定理解三角形,其中方法一 使用余弦定理直接求解,方法二、三,使用反证法,方法二,三比较简单.
分析:方法一:使用余弦定理,由已知求出
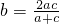 ,计算cosB=
,计算cosB= 的符号,进而可求B的范围
的符号,进而可求B的范围方法二:反证法,假设
 ,则 b为最大边,有b>a>0,b>c>0,结合已知进行推导可求
,则 b为最大边,有b>a>0,b>c>0,结合已知进行推导可求方法三:反证法由题意可得
 =
= ,故b边不是最大边,也不是最小边.假设B≥
,故b边不是最大边,也不是最小边.假设B≥ ,则最大边所对的角大于
,则最大边所对的角大于  ,这与三角形内角和相矛盾,从而可得
,这与三角形内角和相矛盾,从而可得解答:方法一:由题意可得
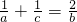 .
.∴
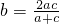 ,
,∵
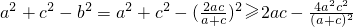 =
=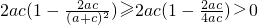 .
.即cosB=
 >0
>0故
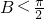
法2:反证法:假设

则有b>a>0,b>c>0.
则
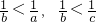
可得
 与已知矛盾,
与已知矛盾,假设不成立,原命题正确.
(法三)∵△ABC的三边a,b,c的倒数成等差数列,
∴
 =
= ,故b边不是最大边,也不是最小边.
,故b边不是最大边,也不是最小边.若B≥
 ,则最大边所对的角大于
,则最大边所对的角大于  ,这与三角形内角和相矛盾,故
,这与三角形内角和相矛盾,故 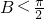 .
.点评:本题主要考查了利用余弦定理解三角形,其中方法一 使用余弦定理直接求解,方法二、三,使用反证法,方法二,三比较简单.

练习册系列答案
相关题目