题目内容
（2012•虹口区二模）函数f(x)=
，则不等式f（x）＞-5的解集是
|
（-1，+∞）
（-1，+∞）
．分析：当x大于等于0时，根据题意得到此时f（x）解析式，代入不等式中，配方后根据完全平方式恒大于0，得到x的取值范围为任意实数，进而确定出此时x的范围，即为所求不等式的解集；当x小于0时，根据题意得到此时f（x）解析式，代入不等式中变形后分解因式，得到x-5与x+1异号，转化为两个一元一次不等式组，求出不等式组的解集得到此时不等式组的解集，确定出所求不等式的解集，综上，得到所求不等式的解集．
解答：解：当x≥0时，f（x）=x2+4x，
不等式化为x2+4x＞-5，即x2+4x+4=（x+2）2＞-1，恒成立，
此时原不等式的解集为[0，+∞）；
当x＜0时，f（x）=4x-x2，不等式化为4x-x2＞-5，即x2-4x-5＜0，
因式分解得：（x-5）（x+1）＜0，
可化为：
或
，
解得：-1＜x＜5，
此时原不等式的解集为（-1，0），
综上，原不等式的解集为（-1，+∞）．
故答案为：（-1，+∞）
不等式化为x2+4x＞-5，即x2+4x+4=（x+2）2＞-1，恒成立，
此时原不等式的解集为[0，+∞）；
当x＜0时，f（x）=4x-x2，不等式化为4x-x2＞-5，即x2-4x-5＜0，
因式分解得：（x-5）（x+1）＜0，
可化为：
|
|
解得：-1＜x＜5，
此时原不等式的解集为（-1，0），
综上，原不等式的解集为（-1，+∞）．
故答案为：（-1，+∞）
点评：此题考查了一元二次不等式的解法，以及分段函数的定义，利用了分类讨论及转化的思想，是高考中常考的题型．
练习册系列答案
相关题目
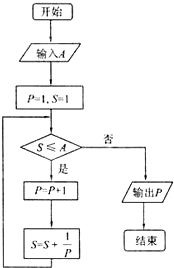（2012•虹口区二模）执行如图所示的程序框图，若输入A的值为2，则输出P的值为