Question

【题目】已知函数

(1) 判断函数的单调性并给出证明；

(2)若存在实数使函数是奇函数，求；

(3)对于(2)中的，若，当时恒成立，求的最大值．

Answer 1

【答案】（1）单调递增（2）见解析

【解析】试题分析：（1）根据单调性定义：先设再作差，变形化为因子形式，根据指数函数单调性确定因子符号，最后根据差的符号确定单调性（2）根据定义域为R且奇函数定义得f(0)＝0，解得a＝1，再根据奇函数定义进行验证（3）先根据参变分离将不等式恒成立化为对应函数最值问题： 的最小值，再利用对勾函数性质得最小值，即得的范围以及的最大值．

试题解析：解：(1)不论a为何实数，f(x)在定义域上单调递增．

证明：设x1，x2∈R，且x1<x2，

则 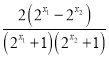由可知，所以,

所以

所以由定义可知，不论为何值， 在定义域上单调递增

(2)由f(0)＝a－1＝0得a＝1，

经验证，当a＝1时， f(x)是奇函数．

(3)由条件可得： m2x＝(2x＋1)＋－3恒成立．m (2x＋1)＋－3的最小值，x∈[2,3]．

设t＝2x＋1，则t∈[5,9]，函数g(t)＝t＋－3在[5,9]上单调递增，

所以g(t)的最小值是g(5)＝，

所以m，即m的最大值是.