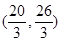题目内容
设函数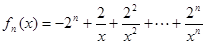 .
.
(1)求函数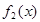 在
在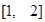 上的值域;
上的值域;
(2)证明对于每一个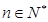 ,在
,在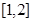 上存在唯一的
上存在唯一的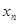 ,使得
,使得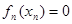 ;
;
(3)求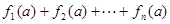 的值.
的值.
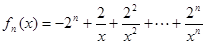 .
.(1)求函数
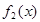 在
在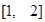 上的值域;
上的值域;(2)证明对于每一个
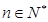 ,在
,在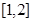 上存在唯一的
上存在唯一的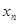 ,使得
,使得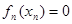 ;
;(3)求
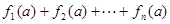 的值.
的值.(1) 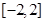 ;(2)证明见解析;(3)当
;(2)证明见解析;(3)当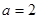 时,为
时,为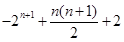 ,当
,当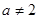 且
且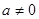 时,为
时,为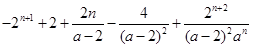 .
.
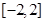 ;(2)证明见解析;(3)当
;(2)证明见解析;(3)当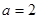 时,为
时,为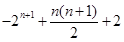 ,当
,当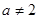 且
且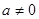 时,为
时,为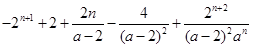 .
.试题分析:(1)由于
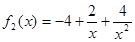 可以看作为
可以看作为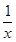 的二次函数,故可利用换元法借助二次函数知识求出值域;(2)这类问题的常用方法是证明
的二次函数,故可利用换元法借助二次函数知识求出值域;(2)这类问题的常用方法是证明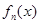 在区间
在区间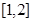 是单调的,且
是单调的,且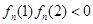 或者
或者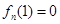 或
或 ,即可得证;本题中证
,即可得证;本题中证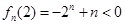 时也可数学归纳法证明;(3)要求
时也可数学归纳法证明;(3)要求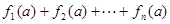 的值,注意分类讨论,
的值,注意分类讨论,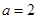 时直接得结论
时直接得结论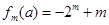 ,那么求
,那么求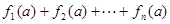 时,只要用分组求和即可,在
时,只要用分组求和即可,在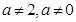 时,
时,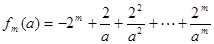 中除第一项外是一个公比不为1的等比数列的和,因此先求出
中除第一项外是一个公比不为1的等比数列的和,因此先求出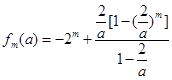
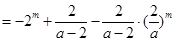 ,同样在求
,同样在求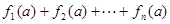 时用分组求和的方法可求得结论.
时用分组求和的方法可求得结论.试题解析:(1)
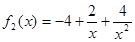 ,由
,由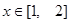 令
令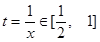 ,
,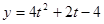 .
.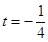 ,
,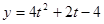 在
在 上单调递增,
上单调递增,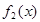 在
在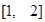 上的值域为
上的值域为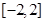 . 4分
. 4分(2)
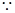 对于
对于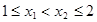 ,
,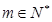 有
有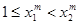 ,
,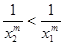 ,从而
,从而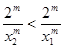 ,
,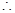
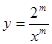 ,
,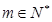 ,在
,在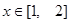 上单调递减,
上单调递减,
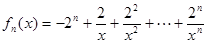 ,
, 在
在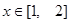 上单调递减.
上单调递减. 又
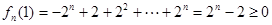 .
.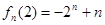 . 7分
. 7分当
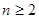 时,
时,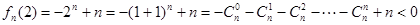
(注用数学归纳法证明
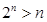 相应给分)
相应给分)又
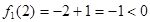 ,即对于任意自然数
,即对于任意自然数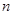 有
有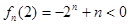
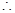 对于每一个
对于每一个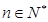 ,存在唯一的
,存在唯一的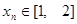 ,使得
,使得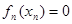 11分
11分(3)
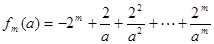 .
.当
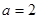 时,
时,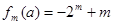 .
.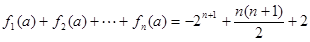 . 14分
. 14分当
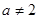 且
且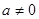 时,
时,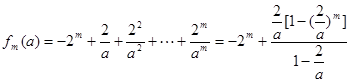 .
.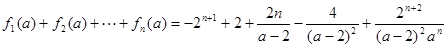 18分
18分
练习册系列答案
相关题目

 ,求
,求 的最大值与最小值;
的最大值与最小值;  的最大值与最小值;
的最大值与最小值;  的图象过点
的图象过点 和
和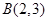 ,则下列各点在函数
,则下列各点在函数



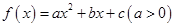 ,当
,当 时,
时, .
. ;
; 成立,请先求出
成立,请先求出 的值,并利用
的值,并利用 的表达式.
的表达式. ,例如:
,例如: ,
,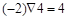 ,则函数
,则函数 的最大值为____________.
的最大值为____________. 对
对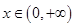 的图象恒在x轴上方,则m的取值范围是( )
的图象恒在x轴上方,则m的取值范围是( )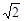 <m<2+2
<m<2+2 (x
(x -2x+3)有以下4个结论:其中正确的有 .
-2x+3)有以下4个结论:其中正确的有 .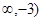
 ; ② 递增区间为
; ② 递增区间为 ;
; 轴的上方.
轴的上方.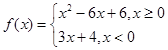 ,若互不相等的实数
,若互不相等的实数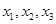 满足
满足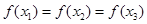 ,则
,则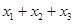 的取值范围是( )
的取值范围是( )